AutomaticMortarGeneration

The AutomaticMortarGeneration class is used to define mortar segment meshes to properly integrate discontinuities caused by normal projections of non-matching, faceted meshes.

2D

Generation of the 2D mortar segment mesh is outlined in Peterson (2018). In short, a nodal-normal projection is used to map points from the primary interface to the secondary interface; secondary interface elements are then split by the projected nodes to form mortar segment mesh elements.

3D

Generation of mortar segment meshes in 3D is more challenging and various approaches exist. In MOOSE we follow the approach suggested in Puso (2004), defining mortar segments on local linearizations of the secondary interface. When the secondary interface is composed entirely of TRI3 faces (which are already linear), generating the mortar segment mesh reduces to projecting the primary face elements onto secondary face elements (along the secondary face normal) and performing a polygon clipping (and subsequent triangularization). The mortar segment mesh is therefore simply a sub-mesh of the secondary mesh in this case.

The definition is more delicate for quadrilateral faces and second order geometries:

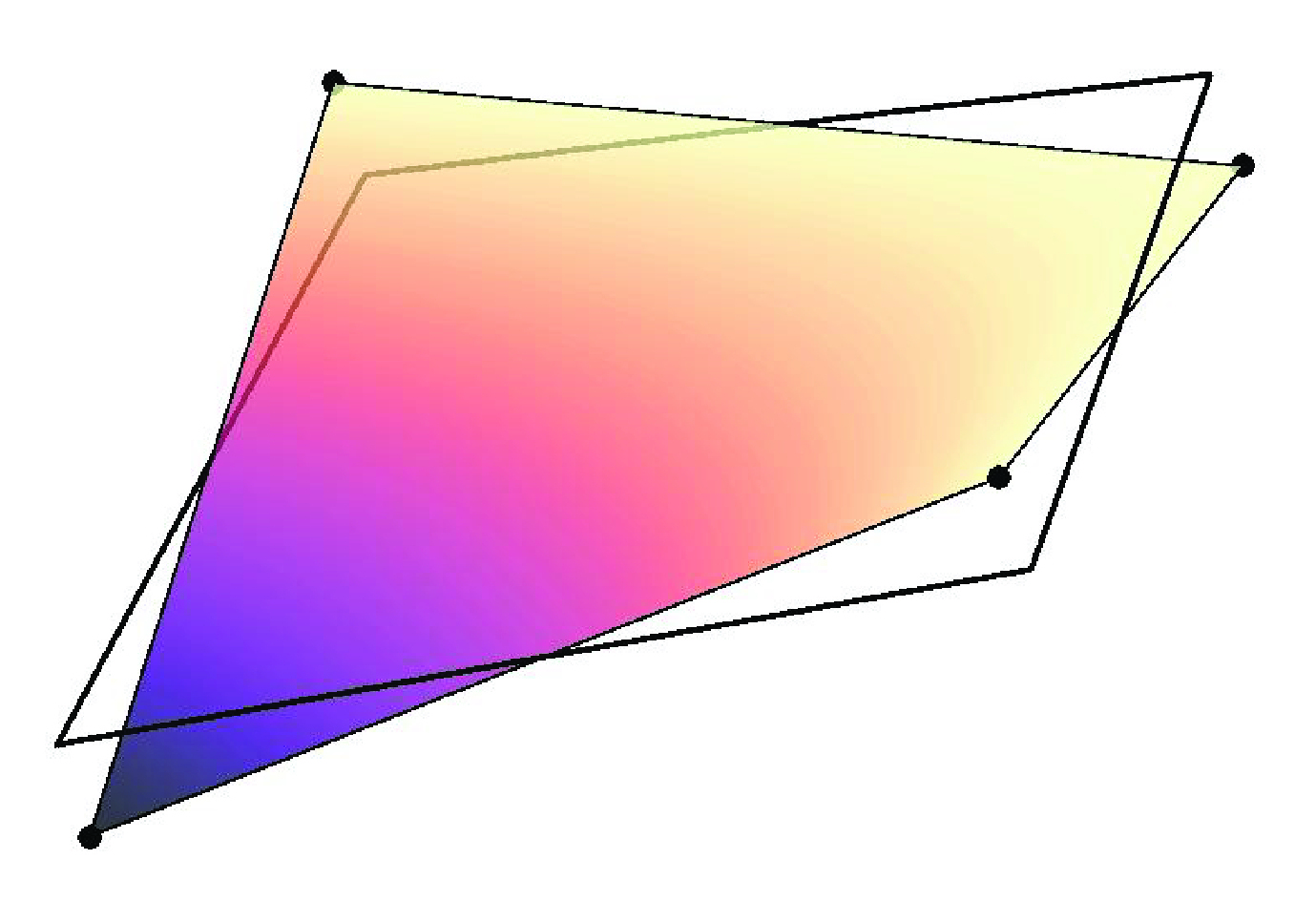
QUAD4 faces

While first-order, QUAD4 faces are (in general) not linear. The 'twisting' or 'potato-chipping' of QUAD4 elements complicates the simple projection and polygon clipping defined for TRI3 faces. To circumvent this problem, mortar segment meshes are defined on local linearizations of QUAD4 elements (see below). The linearization of QUAD4 face elements allows the same polygon clipping algorithm used for TRI3 face elements, but the mortar segment mesh elements produced do not coincide with the secondary mesh and the mortar segment mesh is disconnected between secondary elements.

Second Order Geometries (TRI6 and QUAD9 faces)

Elements defined on second order geometries are curvilinear so to simplify the 'clipping' procedure both secondary and primary face elements are subdivided into first-order face elements then subsequently linearized (illustrated below). The same clipping and triangularization routine is then applied on the linearized sub-elements to create the mortar segments. See Puso et al. (2008).

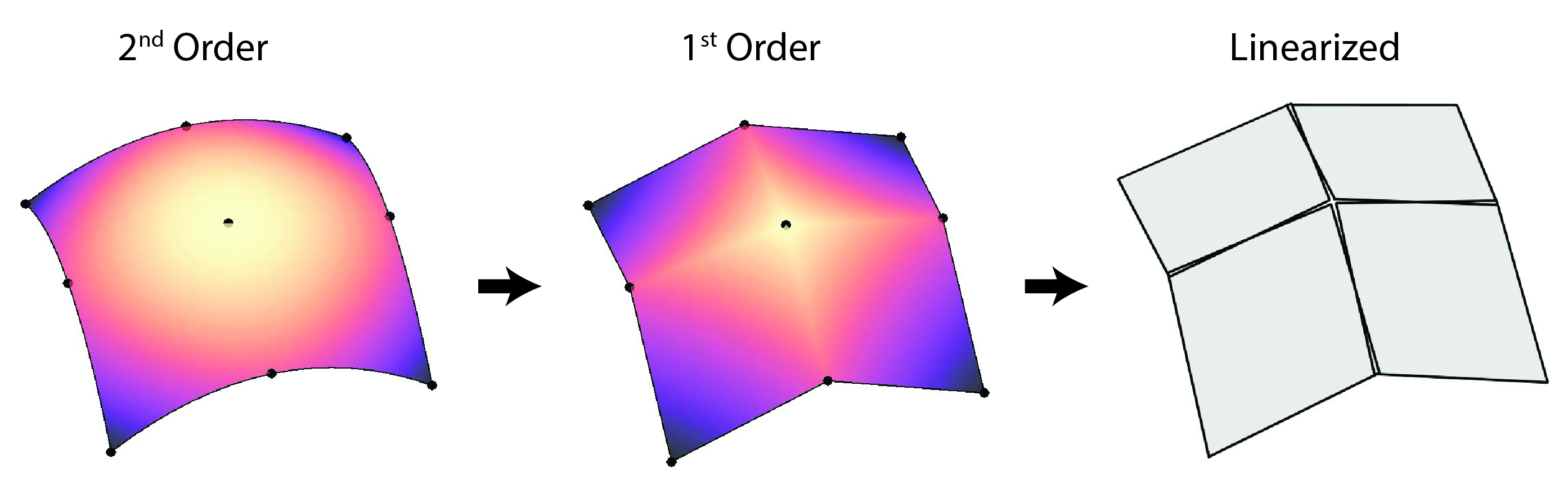
Quadrature points defined on mortar segments (which live on linearized elements) are mapped back to second order elements following an analogous but reverse procedure to the one illustrated above; points are mapped from linearized elements to first order sub-elements then subsequently transformed to the original second order elements.

References

John W. Peterson. Progress toward a new implementation of the mortar finite element method in moose. 2 2018. doi:10.2172/1468630.

@article{osti_1468630,
    author = "Peterson, John W.",
    title = "Progress toward a new implementation of the mortar finite element method in MOOSE",
    abstractNote = {The mortar finite element method has been used for many years in a variety of applications, including the enforcement of continuity conditions across decomposed domains, the implementation of Dirichlet boundary conditions, obtaining improved estimates of surface fluxes, and for solving large deformation contact mechanics problems. There is a currently great deal of interest in developing more robust mechanical and thermal contact solution strategies in the MOOSE framework and physics modules, and schemes based on the mortar finite element approach appear to be a promising avenue of development. There are a number of challenges associated with the development of a robust Lagrange multiplier based formulation of the mortar finite element method which can be tackled using the relatively simple framework of thermal contact problems, before tackling more complicated applications such as thermomechanical contact. In this report, we describe several aspects of our mortar finite element method implementation for solving thermal contact problems. The approach and notation used are based primarily based on the work of Bin Yang et al. ("Two dimensional mortar contact methods for large deformation frictional sliding," International Journal for Numerical Methods in Engineering 62(9), 2005).},
    doi = "10.2172/1468630",
    journal = "",
    place = "United States",
    year = "2018",
    month = "2"
}

Michael A Puso. A 3d mortar method for solid mechanics. International Journal for Numerical Methods in Engineering, 59(3):315–336, 2004.

@article{puso20043d,
    author = "Puso, Michael A",
    title = "A 3D mortar method for solid mechanics",
    journal = "International Journal for Numerical Methods in Engineering",
    volume = "59",
    number = "3",
    pages = "315--336",
    year = "2004",
    publisher = "Wiley Online Library"
}

Michael A Puso, TA Laursen, and Jerome Solberg. A segment-to-segment mortar contact method for quadratic elements and large deformations. Computer Methods in Applied Mechanics and Engineering, 197(6-8):555–566, 2008.

@article{puso2008segment,
    author = "Puso, Michael A and Laursen, TA and Solberg, Jerome",
    title = "A segment-to-segment mortar contact method for quadratic elements and large deformations",
    journal = "Computer Methods in Applied Mechanics and Engineering",
    volume = "197",
    number = "6-8",
    pages = "555--566",
    year = "2008",
    publisher = "Elsevier"
}

2 D
3 D
References