CSGBase
CSGBase is the main class developers should interact with when implementing the generateCSG method for any mesh generator. This framework class acts as a container and driver for all methods necessary for creating a constructive solid geometry (CSG) representation such as generating surfaces, cells, and universes of the mesh generator under consideration.
Throughout this documentation, csg_obj will be used in example code blocks to refer to a CSGBase instance.
Declaring that a mesh generator supports the generation of CSG
In order to call generateCSG, the setHasGenerateCSG method must be called on the mesh generator to declare that the method has been implemented.
InputParameters
TestCSGAxialSurfaceMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
// input parameter that is an existing mesh generator
params.addRequiredParam<MeshGeneratorName>("input", "The input MeshGenerator.");
// additional params for this specific mesh generator
params.addRequiredParam<Real>("axial_height", "Axial height of the model.");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
How to implement the generateCSG routine
This section will describe the various components developers should implement into the generateCSG method for a given MeshGenerator. This method will return a unique pointer to the CSGBase object that was created or modified by the mesh generator in the generateCSG method.
Initialization
A new CSGBase object can be initialized with:
auto csg_obj = std::make_unique<CSG::CSGBase>();
Once initialized, surfaces, cells, and universes can be created and manipulated. The following sections explain in detail how to do this as a part of the generateCSG method.
Surfaces
Surfaces are used to define the spatial extent of the region of a CSGCell. To create a CSGSurface object, the surface constructor must be called directly to create a unique pointer. This pointer then has to be passed to the current CSGBase instance with addSurface which will then return a const reference to that generated surface (const & CSGSurface). The syntax to do this is as follows, where SurfaceType should be replaced with the specific type of surface being created (e.g., CSG::CSGPlane):
// the unique surface pointer is made first, creating the surface object
std::unique_ptr<CSG::CSGSurface> surf_ptr = std::make_unique<SurfaceType>(arguments);
// and then it is explicitly passed to this CSGBase instance, which holds the memory ownership for the object
const auto & surface = csg_obj->addSurface(std::move(surf_ptr));
Surfaces need to be added to the CSGBase instance with addSurface as described above. If this is not done and these surfaces are referenced in regions used to define cells within the CSGBase instance, an error will occur.
The CSG framework in MOOSE provides various classes for creating basic surfaces (see table below). Information about how to define new types of surfaces can be found in CSGSurface.
| Surface Type | Class | Description |
|---|---|---|
| Plane | CSGPlane | create a plane defined by 3 points or from coefficients a, b, c, and d for the equation ax + by + cz = d |
| Sphere | CSGSphere | creates a sphere of radius r at an optionally specified center point (default is (0, 0, 0)) |
| Cylinder | CSGXCylinder | creates a cylinder aligned with the x-axis at the specified center location (y, z) |
| Cylinder | CSGYCylinder | creates a cylinder aligned with the y-axis at the specified center location (x, z) |
| Cylinder | CSGZCylinder | creates a cylinder aligned with the z-axis at the specified center location (x, y) |
Example:
// create a plane using the coefficients for the equation of a plane
// z plane equation: 0.0*x + 0.0*y + 1.0*z = (+/-)0.5 * axial_height
std::unique_ptr<CSG::CSGSurface> surface_ptr =
std::make_unique<CSG::CSGPlane>(default_surf_name, 0.0, 0.0, 1.0, coeffs[i]);
auto & csg_plane = csg_obj->addSurface(std::move(surface_ptr));
In order to define a surface, the header file for that surface type must be included in the MeshGenerator.C file (i.e., #include "CSGPlane.h" to create planes).
The CSGSurface objects can then be accessed or updated with the following methods from CSGBase:
addSurface: add a unique pointer to aCSGSurfaceobject to thisCSGBaseinstancegetAllSurfaces: retrieve a list of const references to eachCSGSurfaceobject in theCSGBaseinstancegetSurfaceByName: retrieve a const reference to theCSGSurfaceof the specified namerenameSurface: change the name of theCSGSurface
Regions
A region is a space defined by boolean operations applied to surfaces and other regions. Half-space regions are defined as the positive and negative space separated by a surface. These regions can be unionized, intersected, or the complement taken to further define more complex regions. Series of operations can be defined using parentheses ( ) to indicate which operations to perform first. The types of operators available to define a CSGRegion using CSGSurface objects are:
| Operator | Description | Example Use |
|---|---|---|
+ | positive half-space | +surf |
- | negative half-space | -surf |
& | intersection | -surfA & +surfB |
| | union | -surfA | +surfB |
~ | complement | ~(-surfA & +surfB) |
&= | update existing region with an intersection | region1 &= -surfA |
|= | update existing region with a union | region1 |= +surfB |
The following is an example of using a combination of all operators to define the space outside a cylinder of a finite height that is topped with a half-sphere. Each of the half-spaces associated with each surface are shown in Figure 1. The cylinder and planes are then combined via intersection to form the region inside a finite cylinder, and the space above the top plane is intersected with the sphere to define a half sphere (Figure 2). These two regions are unionized as shown in Figure 3. The complement of the previous combination then defines the final region ~((-cylinder_surf & -top_plane & +bottom_plane) | (+top_plane & -sphere_surf)), as shown in blue in Figure 4.
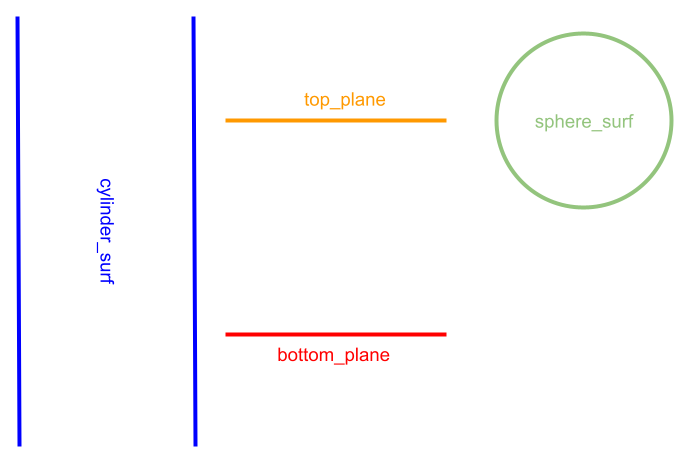
Figure 1: Four different surfaces: an infinite cylinder (blue), a top plane (orange), a bottom plane (red), and a sphere (green)
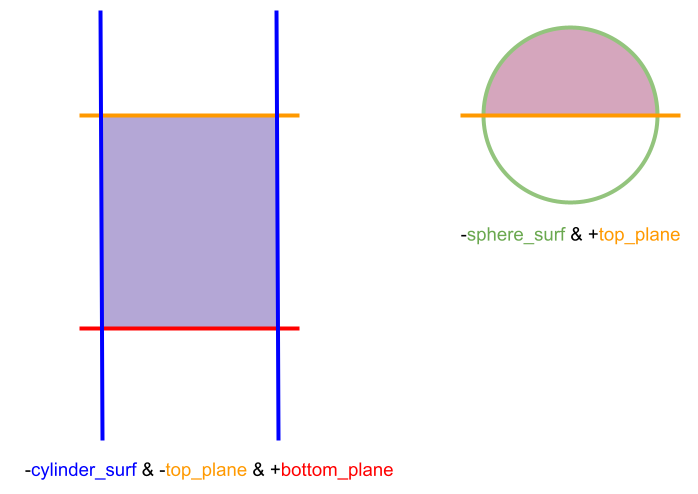
Figure 2: Two separate regions both defined as intersections of half-spaces.
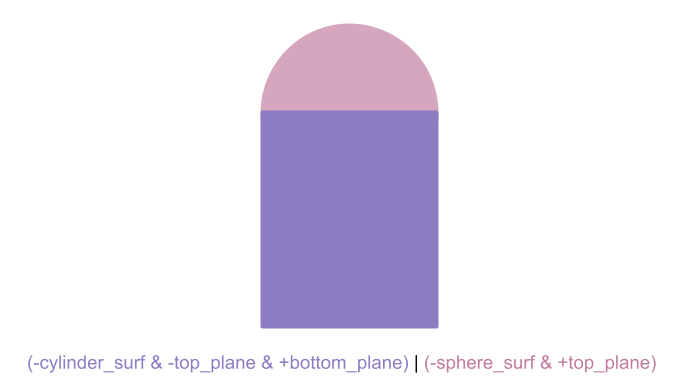
Figure 3: One region defined by the union of two other regions.

Figure 4: A region defined as the complement of an existing region.
Cells
A cell is an object defined by a region and a fill. To create any CSGCell, use the method createCell from CSGBase which will return a const reference to the CSGCell object that is created (const CSGCell &). At the time of calling createCell, a unique cell name, the cell region (CSGRegion), and an indicator of the fill must be provided. The CSGRegion is defined by boolean combinations of CSGSurfaces as described below. Four types of cell fills are currently supported: void, material, universe, and lattice. If creating a void cell, no fill has to be passed to the creation method. To create a cell with a material fill, simply provide it with a name of a material as a string. For a cell with a CSGUniverse fill, pass it a reference to the CSGUniverse. And for a CSGLattice fill, pass a reference to the CSGLattice. Some examples of creating the different types of cells are shown below:
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
A cell with a material fill is not connected to a MOOSE material definition at this time. The "material" is currently just a string to represent the name of a CSG material or other type of fill that is otherwise undefined.
The CSGCell objects can then be accessed or updated with the following methods from CSGBase:
getAllCells: retrieve a list of const references to eachCSGCellobject in theCSGBaseinstancegetCellByName: retrieve a const reference to theCSGCellobject of the specified namerenameCell: change the name of theCSGCellobjectupdateCellRegion: change the region of the cell; if used, allCSGSurfaceobjects used to define the newCSGRegionmust also be a part of the currentCSGBase
Universes
A universe is a collection of cells and is created by calling createUniverse from CSGBase which will return a const reference to the CSGUniverse object (const CSGUniverse &). A CSGUniverse can be initialized as an empty universe, or by passing a vector of shared pointers to CSGCell objects. Any CSGUniverse object can be renamed (including the root universe) with renameUniverse.
The CSGUniverse objects can then be accessed or updated with the following methods from CSGBase:
getAllUniverses: retrieve a list of const references to eachCSGUniverseobject in theCSGBaseinstancegetUniverseByName: retrieve a const reference to theCSGUniverseof the specified namerenameUniverse: change the name of theCSGUniverse
Examples:
auto new_univ = csg_obj->createUniverse("new_univ");
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
Root Universe
All universes in a model should be able to be traced back, through the hierarchical tree of cells and universes, to a singular overarching universe known as the root universe. Because universes are a collection of cells and cells can be filled with universe, a tree of universes can be constructed such that the root universe contains the collection of all cells in the model. When a CSGBase object is first initialized, a root CSGUniverse called ROOT_UNIVERSE is created by default. Every CSGCell that is created will be added to the root universe unless otherwise specified (as described below). The root universe exists by default, and which universe is set as the root cannot be changed, except when joining CSGBase objects, as described below. However, the name of the root universe can be updated and cells can be manually added or removed using the same methods described above.
Methods available for managing the root universe:
getRootUniverse: returns a const reference to the root universe of theCSGBaseinstancerenameRootUniverse: change the name of the root universe
Adding or Removing Cells
There are multiple ways in which cells can be added to a universe:
At the time of universe creation, a vector of references to
CSGCellobjects can be passed intocreateUniverse(as described above). Example:
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
When a
CSGCellis created withcreateCell, a pointer to aCSGUniversecan be passed as the final argument to indicate that the cell will be created and added directly to that specified universe. In this case, the cell will not be added to the root universe. A cell that has a universe fill type cannot be added to the same universe that is being used for the fill. For example, the two snippets below come from the same file where a new universe is initialized and passed by reference to the cell when it is created:
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
A cell or list of cells can be added to an existing universe with the
addCellToUniverseandaddCellsToUniversemethods. In this case, if aCSGCellexists in anotherCSGUniverse(such as the root universe), it will not be removed when being added to another (i.e. if the same behavior as option 2 above is desired, the cell will have to be manually removed from the root universe, as described below). The following is an example where the list of cells is collected first and then added at one time to the existing universe, but this could also be accomplished by usingaddCellToUniversein a for-loop after each cell is initially created.
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
Cells can also be removed from a universe in the same way as method 3 above by using the removeCellFromUniverse and removeCellsFromUniverse methods. An example is shown above where the cells are removed from the root universe after they are added to the new universe. Doing this in multiple steps has the same outcome as that of method 2 for adding cells to a universe at the time of cell creation.
When adding and removing cells to/from universes, it is important to maintain the connectivity of all universes meaning all universes should be nested under the root universe at the end of the generation process, in order to have a consistent model.
Lattices
A CSGLattice is defined as a patterned arrangement of CSGUniverse objects and an "outer" to fill the space around lattice elements. To create any type of lattice, the lattice constructor must be called directly to create a unique pointer. This pointer then has to be passed to the current CSGBase instance with addLattice (optionally specifying the lattice type) which will then return a const reference to that generated lattice object (const & CSGLattice or const & LatticeType). At the time that addLattice is called to add the lattice to the base instance, any CSGUniverse objects associated with the lattice must also be in the CSGBase instance already. The syntax for creating the pointer and adding it is shown below, where LatticeType should be replaced with the specific type of the lattice (e.g., CSGCartesianLattice or CSGHexagonalLattice).
// the unique lattice pointer is made first, creating the lattice object of the specified type
std::unique_ptr<LatticeType> lat_ptr = std::make_unique<LatticeType>(arguments);
// and then it is explicitly passed to this CSGBase instance, which will keep the memory ownership for the object
const auto & lattice = csg_obj->addLattice<LatticeType>(std::move(lat_ptr));
An example of creating a Cartesian lattice is shown below:
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>(lat_name, _pitch, universe_pattern);
csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
It is _highly_ recommended that the specific LatticeType of the lattice object always be specified when calling addLattice or getLatticeByName. If it is not specified, it will default to setting the type as the abstract type CSGLattice. If this is the case, no methods or data that is specific to the actual lattice type will be callable on the lattice object, unless a reference cast is used.
The CSGBase class provides support for two types of 2D lattice types (Cartesian and regular hexagonal), but any custom lattice type can also be defined by following the information in CSGLattice. It is assumed that both the Cartesian and hexagonal lattice types are in the plane (having a normal). Three types of outer fill are supported: void (default), material (an std::string name), and CSGUniverse. For both lattice types, the lattice can be initialized minimally with a name and pitch (the flat-to-flat size of a lattice element). The pattern of universes can also be set at the time of initialization or updated later using the setLatticeUniverses method. And similarly, the outer fill (either a CSGUniverse object or an std::string representing the name of a material) can be set at the time of initialization or set later with the setLatticeOuter method; if the outer is not set, it is assumed to be VOID. Some examples of initializing a lattice with the various options are shown below.
// initialize without universe map, outer is void, and pitch=1.0
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
// initialize with universe map and set outer fill to be a universe
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map, outer_univ);
// initialize without universe map but set outer to a material
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, "outer_mat");
The CSGBase class supports only the creation of 2D lattices. A "3D" lattice can be created by filling multiple 3D cells with 2D lattices and arranging them in layers to form the desired 3D structure.
The CSGLattice objects can be accessed or updated with the following methods from CSGBase:
setLatticeUniverses: sets the vector of vectors ofCSGUniverseobjects as the lattice layout.setUniverseAtLatticeIndex: add aCSGUniverseto the lattice at the specified location index (replaces the existing universe).setLatticeOuter: sets theCSGUniverse(for aCSGUniverseouter) or thestd::stringname (for a material outer) as the outer fill.resetLatticeOuter: resets the outer fill to void for the lattice.renameLattice: change the name of theCSGLatticeobject.getAllLattices: retrieve a vector of const references to eachCSGLatticeobject in theCSGBaseinstance.getLatticeByName: retrieve a const reference to the lattice object of the specified name.
Lattice Indexing
Both the Cartesian and hexagonal lattice types follow a row-column indexing scheme for the location of universes in the lattice.
For Cartesian lattices, there can be any number of rows and columns, but each row must be the same length. The indexing starts at the top left corner of the lattice with element . An example of the indices for a Cartesian lattice is shown in Figure 5.
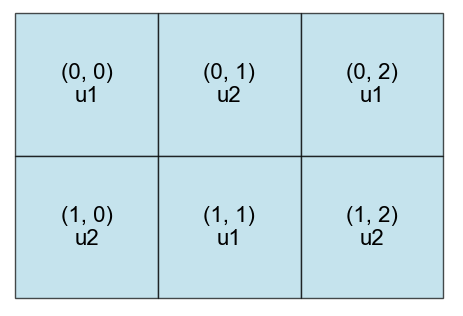
Figure 5: Example of a Cartesian lattice and the corresponding location indices.
For hexagonal lattices, the lattice is assumed to be x-oriented and also uses the row-column indexing scheme, with element being the top row, leftmost element. The length of the rows is expected to be consistent with the size of the lattice (i.e., the number of rings), which is verified when the universes are set. An example of the indices for a 3-ring hexagonal lattice is shown in Figure 6.
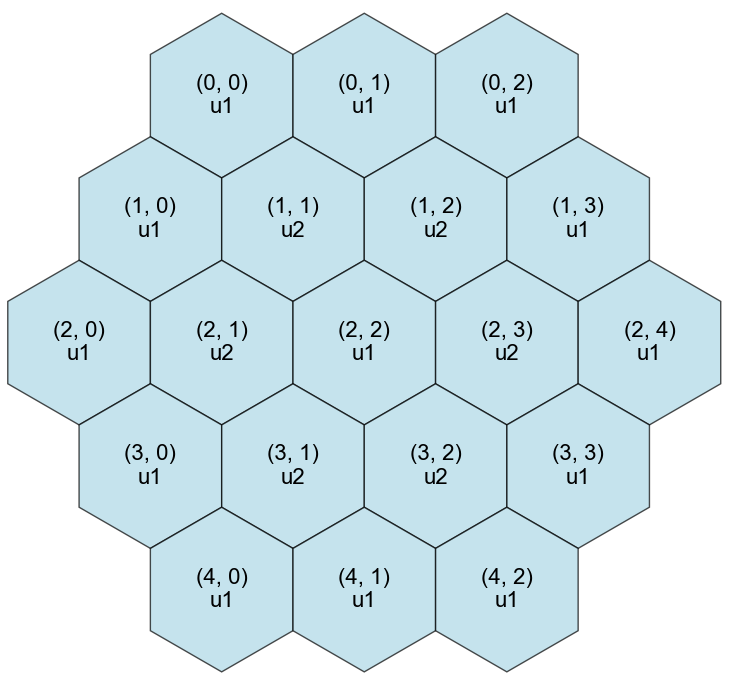
Figure 6: Example of a 3-ring hexagonal lattice that has the location indices labeled in the form.
Convenience methods are provided for CSGHexagonalLattice objects to convert between the required indices and a ring-based indexing scheme. In the ring-based scheme, the outermost ring is the 0th ring, and the right-most element in the ring is the 0th position of the ring with indices increasing counter-clockwise around the ring. For the 3-ring lattice above in Figure 6, the corresponding indices would be as shown in Figure 7.
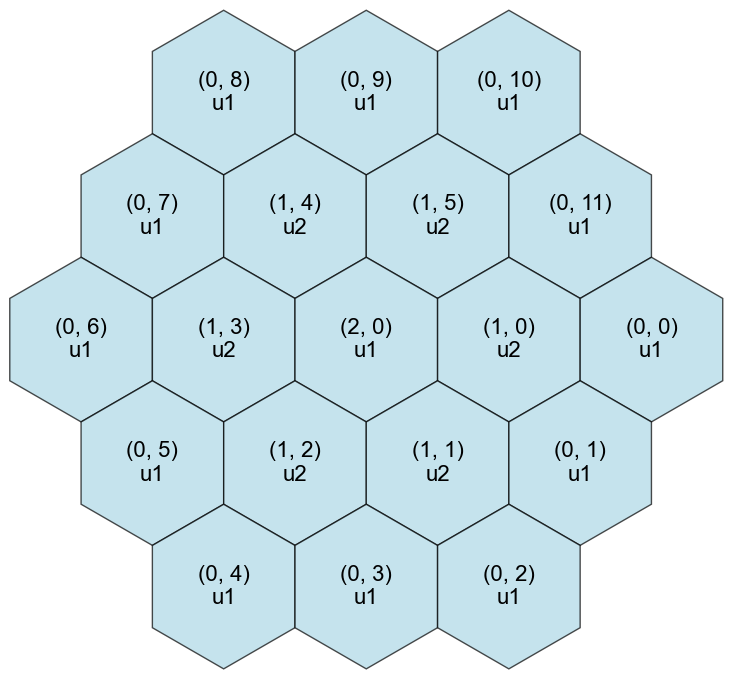
Figure 7: Example of a 3-ring hexagonal lattice that has the location indices labeled in the form.
For any lattice, the index of a universe in the lattice can be retrieved from the index by calling the getRingIndexFromRowIndex method. And similarly, if the index form is known, the corresponding index can be retrieved using the getRowIndexFromRingIndex method. It is important to note that while these convenience methods exist to convert between the two indexing schemes, the CSGUniverse objects in the lattice can only be accessed using the index.
Defining the Universe Layout
As mentioned above, the layout of the CSGUniverse objects for the lattice can be set at the time of initialization or set/updated later. At the time that the universes are set, the dimensionality of the lattice is determined (i.e., the number of rows, columns, or rings for the lattice). If the dimensionality should need to be changed, a new complete universe arrangement can be set to overwrite the previous arrangement using setLatticeUniverses. Anytime the universe layout is set or changed, the dimensionality will be validated to ensure it compatible with the lattice type. To replace a single element of the lattice, the setUniverseAtLatticeIndex method can be used by providing the element location in form. In order to use this method, the full set of universes must have already been defined, either during the lattice initialization or with setLatticeUniverses.
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
The setUniverseAtLatticeIndex method is not meant to be used to change a lattice's dimensions by building the lattice element-by-element because the index supplied would be considered out of range in this context. The dimensionality of the lattice is determined when setLatticeUniverses is called. Therefore, to build a lattice incrementally, the recommendation is to build up a vector of vectors of universes incrementally and then call setLatticeUniverses one time. From there, setUniverseAtLatticeIndex can be called to replace an existing universe in the lattice.
Updating Existing CSGBase Objects
An empty CSGBase object can be initialized on its own in each generateCSG method for each mesh generator. However, in most cases, it is necessary to update an existing CSGBase object from a previous MeshGenerator or join multiple CSGBase together such that only one CSGBase object is ultimately produced at the end of the mesh/CSG generation process. There are two main ways to handle this: passing and joining.
Passing between Mesh Generators
CSGBase objects from other mesh generators can be accessed through methods that parallel those available for accessing other MeshGenerator objects. For all methods listed below, a unique pointer to the CSGBase object(s) created by generateCSG for the specified MeshGenerator names are returned.
getCSGBase: get theCSGBaseobject given a parameter name represented as astd::stringthat stores the mesh generator namegetCSGBases: get theCSGBaseobjects given a parameter name represented as astd::stringthat stores a list of mesh generator namesgetCSGBaseByName: get theCSGBaseobject given aMeshGeneratorNamegetCSGBasesByName: get allCSGBaseobjects given a list ofMeshGeneratorNames
These functions should be called from the constructor of the MeshGenerator, so that the MeshGenerator system can properly define the dependency tree of all mesh generators in the input file. The returned CSGBase pointers can be stored in a member variable and updated in the generateCSG() method in order to make any changes to the CSGBase object.
For example, the following member variable stores the pointer to the CSGBase object that is generated by an input mesh generator:
/// Holds the generated CSGBase object
std::unique_ptr<CSG::CSGBase> * _build_csg;
This variable is initialized in the constructor as:
_build_csg = &getCSGBase("input");
Finally, in the generateCSG() method, std::move is called on the member variable to transfer ownership to the current mesh generator
// get the existing CSGBase associated with the input mesh generator
// this is the CSGBase object that will be updated
std::unique_ptr<CSG::CSGBase> csg_obj = std::move(*_build_csg);
A MeshGenerator object(s) can be passed to another mesh generator as input by providing InputParameters of type MeshGeneratorName. See the ExampleAxialSurfaceMeshGenerator implementation below for an example of this.
Joining Bases
When two or more existing CSGBase objects need to be combined to continue to use and update, the joinOtherBase method should be used. This method is called from another CSGBase and at a minimum takes a different existing CSGBase object as input. There are 3 different behaviors for joining bases that are supported depending on the additional arguments that are passed:
No additional arguments: All cells that are in the root universe of the incoming
CSGBaseobject will be added to the existing root universe of the current base object, and the root universe from the incoming base will no longer exist.
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
One new root universe name (
new_root_name_join): All cells in the root universe of the incoming base will be used to create a new universe of the name specified by thenew_root_name_joinparameter. These cells will not be added to the existing root universe, which will remain unchanged. This new universe will be added as a new non-root universe in the existing base object. This newly created universe will not be connected to the root universe of the existingCSGBaseobject by default.
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
Two new root universe names (
new_root_name_baseandnew_root_name_join): The cells in the root universe of the currentCSGBaseobject will be used to create a new non-root universe of the name specified by thenew_root_name_baseparameter, and the cells in the root universe of the incomingCSGBaseobject will be used to create a separate non-root universe of the name specified by thenew_root_name_joinparameter. At the end of this join method, the root universe of the current base object will be empty and neither of the two new non-root universes will be connected to the root universe by default.
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
For all of these join methods, any non-root universes will remain unchanged and simply added to the list of universes for the current CSGBase object. Similarly, all incoming cells and surfaces are added alongside existing cells and surfaces.
It is very important when using the joinOtherBase method that all CSGSurfaces, CSGCells, and CSGSurfaces are uniquely named so that errors are not encountered when combining sets of objects. An error will be produced during the join process if an object of the same type and name already exists. See recommendations for naming below.
Accessing CSG-related Methods
All Constructive Solid Geometry (CSG) methods related to creating or changing a CSG object must be called through CSGBase. Calls that retrieve information only but do not manipulate an object (such as getName methods) can be called on the object directly. For example, if a cell were to be created, the current name and region could be retrieved directly from the CSGCell object, but if the name or region needed to be changed, that would need to be handled through CSGBase.
This ensures proper accounting of all CSG-related objects in the CSGBase instance. Consult the Doxygen documentation for information on all object-specific methods.
Object Naming Recommendations
For each new CSG element (CSGSurface, CSGCell, CSGUniverse, and CSGLattice) that is created, a unique name identifier (of type std::string) must be provided (name parameter for all creation methods). A recommended best practice is to include the mesh generator name (which can be accessed with this->getName() in any MeshGenerator class) as a part of that object name. This name is used as the unique identifier within the CSGBase instance. Methods for renaming objects are available as described in the above sections to help prevent issues and errors.
Example Implementations
Provided here are example implementations of the generateCSG method for three simple MeshGenerator types. The first mesh generator creates an infinite rectangular prism given an input parameter for side_length. The code snippets provided here correspond to the .C file.
InputParameters
ExampleCSGInfiniteSquareMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
params.addRequiredParam<Real>("side_length", "Side length of infinite square.");
params.addParam<MeshGeneratorName>(
"fill", "optional input lattice mesh generator to fill generated cell with.");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
ExampleCSGInfiniteSquareMeshGenerator::ExampleCSGInfiniteSquareMeshGenerator(
const InputParameters & params)
: MeshGenerator(params),
_side_length(getParam<Real>("side_length")),
_input_fill_name(isParamValid("fill") ? getParam<MeshGeneratorName>("fill") : ""),
_has_fill(isParamValid("fill"))
{
if (_has_fill)
{
_input_fill_mg_ptr = &getMesh("fill");
_input_fill_csg = &getCSGBase("fill");
}
}
std::unique_ptr<MeshBase>
ExampleCSGInfiniteSquareMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
ExampleCSGInfiniteSquareMeshGenerator::generateCSG()
{
// name of the current mesh generator to use for naming generated objects
auto mg_name = this->name();
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// Add surfaces and halfspaces corresponding to 4 planes of infinite square
std::vector<std::vector<Point>> points_on_planes{{Point(1. * _side_length / 2., 0., 0.),
Point(1. * _side_length / 2., 1., 0.),
Point(1. * _side_length / 2., 0., 1.)},
{Point(-1. * _side_length / 2., 0., 0.),
Point(-1. * _side_length / 2., 1., 0.),
Point(-1. * _side_length / 2., 0., 1.)},
{Point(0., 1. * _side_length / 2., 0.),
Point(1., 1. * _side_length / 2., 0.),
Point(0., 1. * _side_length / 2., 1.)},
{Point(0., -1. * _side_length / 2., 0.),
Point(1., -1. * _side_length / 2., 0.),
Point(0., -1. * _side_length / 2., 1.)}};
std::vector<std::string> surf_names{"plus_x", "minus_x", "plus_y", "minus_y"};
// initialize cell region to be updated
CSG::CSGRegion region;
// set the center of the prism to be used for determining half-spaces
const auto centroid = Point(0, 0, 0);
for (unsigned int i = 0; i < points_on_planes.size(); ++i)
{
// object name includes the mesh generator name for uniqueness
const auto surf_name = mg_name + "_surf_" + surf_names[i];
// create the plane for one face of the prism
std::unique_ptr<CSG::CSGSurface> plane_ptr = std::make_unique<CSG::CSGPlane>(
surf_name, points_on_planes[i][0], points_on_planes[i][1], points_on_planes[i][2]);
auto & csg_plane = csg_obj->addSurface(std::move(plane_ptr));
// determine where the plane is in relation to the centroid to be able to set the half-space
const auto region_direction = csg_plane.getHalfspaceFromPoint(centroid);
// half-space is either positive (+plane_ptr) or negative (-plane_ptr)
// depending on the direction to the centroid
auto halfspace =
((region_direction == CSG::CSGSurface::Halfspace::POSITIVE) ? +csg_plane : -csg_plane);
// check if this is the first half-space to be added to the region,
// if not, update the existing region with the intersection of the regions (&=)
if (region.getRegionType() == CSG::CSGRegion::RegionType::EMPTY)
region = halfspace;
else
region &= halfspace;
}
// create the cell defined by the surfaces and region just created
const auto cell_name = mg_name + "_square_cell";
// determine fill: either from input fill mesh generator or default material
if (_has_fill)
{
// join the fill CSGBase into the current CSGBase & use the lattice as the fill
csg_obj->joinOtherBase(std::move(*_input_fill_csg));
// assume input MG is a lattice type for sake of this example/test
const CSG::CSGLattice & lattice = csg_obj->getLatticeByName(_input_fill_name + "_lattice");
csg_obj->createCell(cell_name, lattice, region);
}
else // default material fill
{
const auto material_name = "square_material";
csg_obj->createCell(cell_name, material_name, region);
}
return csg_obj;
}
The next example mesh generator builds on the infinite prism example above by taking a MeshGeneratorName for an existing ExampleCSGInfiniteSquareMeshGenerator as input and adds planes to create a finite rectangular prism.
InputParameters
TestCSGAxialSurfaceMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
// input parameter that is an existing mesh generator
params.addRequiredParam<MeshGeneratorName>("input", "The input MeshGenerator.");
// additional params for this specific mesh generator
params.addRequiredParam<Real>("axial_height", "Axial height of the model.");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
TestCSGAxialSurfaceMeshGenerator::TestCSGAxialSurfaceMeshGenerator(const InputParameters & params)
: MeshGenerator(params),
_mesh_ptr(getMesh("input")),
_axial_height(getParam<Real>("axial_height"))
{
_build_csg = &getCSGBase("input");
}
std::unique_ptr<MeshBase>
TestCSGAxialSurfaceMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
TestCSGAxialSurfaceMeshGenerator::generateCSG()
{
// get the existing CSGBase associated with the input mesh generator
// this is the CSGBase object that will be updated
std::unique_ptr<CSG::CSGBase> csg_obj = std::move(*_build_csg);
// get the names of the current mesh generator and the input mesh generator
// so that unique object naming can be enforced
auto mg_name = this->name();
auto inp_name = getParam<MeshGeneratorName>("input");
// get the expected existing cell
const auto cell_name = inp_name + "_square_cell";
const auto & csg_cell = csg_obj->getCellByName(cell_name);
// get the existing cell region to update
auto cell_region = csg_cell.getRegion();
// centroid used to determine direction for half-space
const auto centroid = Point(0, 0, 0);
// setting a default surface name purely for testing purposes
const auto default_surf_name = "default_surf";
// Add surfaces and halfspaces corresponding to top and bottom axial planes
std::vector<std::string> surf_names{"plus_z", "minus_z"};
std::vector<Real> coeffs{0.5 * _axial_height, -0.5 * _axial_height};
for (unsigned int i = 0; i < coeffs.size(); ++i)
{
// create a plane using the coefficients for the equation of a plane
// z plane equation: 0.0*x + 0.0*y + 1.0*z = (+/-)0.5 * axial_height
std::unique_ptr<CSG::CSGSurface> surface_ptr =
std::make_unique<CSG::CSGPlane>(default_surf_name, 0.0, 0.0, 1.0, coeffs[i]);
auto & csg_plane = csg_obj->addSurface(std::move(surface_ptr));
// Rename surface so that it has a unique surface name based on the mesh generator
const auto surf_name = mg_name + "_surf_" + surf_names[i];
csg_obj->renameSurface(csg_plane, surf_name);
// determine the half-space to add as an updated intersection
const auto region_direction = csg_plane.getHalfspaceFromPoint(centroid);
auto halfspace =
((region_direction == CSG::CSGSurface::Halfspace::POSITIVE) ? +csg_plane : -csg_plane);
// update the existing region with a half-space
cell_region &= halfspace;
}
// set the new region for the existing cell
csg_obj->updateCellRegion(csg_cell, cell_region);
// Rename cell as it now defines a box region instead of an infinite square region
csg_obj->renameCell(csg_cell, mg_name + "_box_cell");
return csg_obj;
}
If the above methods were to be used, the following input would generate the corresponding JavaScript Object Notation (JSON) output below.
Example Input:
[Mesh<<<{"href": "../../syntax/Mesh/index.html"}>>>]
[inf_square]
type = ExampleCSGInfiniteSquareMeshGenerator
side_length = 4
[]
[cube]
type = TestCSGAxialSurfaceMeshGenerator
input = inf_square
axial_height = 5
[]
[]Example Output:
{
"cells": {
"cube_box_cell": {
"fill": "square_material",
"filltype": "CSG_MATERIAL",
"region":
"(+inf_square_surf_plus_x & -inf_square_surf_minus_x & -inf_square_surf_plus_y & +inf_square_surf_minus_y & -cube_surf_plus_z & +cube_surf_minus_z)"
}
},
"surfaces": {
"inf_square_surf_minus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": 2.0
},
"type": "CSG::CSGPlane"
},
"inf_square_surf_minus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": -2.0
},
"type": "CSG::CSGPlane"
},
"cube_surf_minus_z": {
"coefficients": {
"a": 0.0,
"b": 0.0,
"c": 1.0,
"d": -2.5
},
"type": "CSG::CSGPlane"
},
"inf_square_surf_plus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": -2.0
},
"type": "CSG::CSGPlane"
},
"inf_square_surf_plus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": 2.0
},
"type": "CSG::CSGPlane"
},
"cube_surf_plus_z": {
"coefficients": {
"a": 0.0,
"b": 0.0,
"c": 1.0,
"d": 2.5
},
"type": "CSG::CSGPlane"
}
},
"universes": {
"ROOT_UNIVERSE": {
"cells": [
"cube_box_cell"
],
"root": true
}
}
}
A third example implementation shows the construction of a 2D lattice of universes, using the ExampleCSGInfiniteSquareMeshGenerator as input.
InputParameters
TestCSGLatticeMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
// input parameter that is an existing mesh generator
params.addRequiredParam<std::vector<MeshGeneratorName>>(
"inputs",
"The MeshGenerators that form the components of the lattice. Order of inputs corresponds to "
"the associated integer ID for the pattern (i.e., 0 for first input, 1 for second input, "
"etc.)");
params.addRequiredParam<std::string>(
"lattice_type", "The type of lattice to create. Options are 'cartesian' and 'hexagonal'.");
params.addRequiredParam<Real>("pitch",
"The pitch (flat-to-flat distance) of each lattice element.");
params.addRequiredParam<std::vector<std::vector<unsigned int>>>(
"pattern",
"A double-indexed array starting with the upper-left corner where the index"
"represents the index of the mesh/CSG generator in the 'inputs' vector");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
TestCSGLatticeMeshGenerator::TestCSGLatticeMeshGenerator(const InputParameters & params)
: MeshGenerator(params),
_lattice_type(getParam<std::string>("lattice_type")),
_pitch(getParam<Real>("pitch")),
_input_names(getParam<std::vector<MeshGeneratorName>>("inputs")),
_mesh_ptrs(getMeshes("inputs")),
_pattern(getParam<std::vector<std::vector<unsigned int>>>("pattern"))
{
for (auto inp : _input_names)
_input_csgs.push_back(&getCSGBaseByName(inp));
}
std::unique_ptr<MeshBase>
TestCSGLatticeMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
TestCSGLatticeMeshGenerator::generateCSG()
{
// create a new CSGBase object to build the lattice in
auto csg_obj = std::make_unique<CSG::CSGBase>();
// get the name of the current mesh generator
auto mg_name = this->name();
// join each input CSGBase into the new CSGBase as a unique universe
std::unordered_map<unsigned int, std::string> univ_id_names;
for (const auto i : index_range(_input_names))
{
std::string join_name = _input_names[i] + "_univ";
csg_obj->joinOtherBase(std::move(*_input_csgs[i]), join_name);
univ_id_names[i] = join_name;
}
// build the universe pattern for the lattice using the input pattern
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> universe_pattern;
for (const auto & row : _pattern)
{
std::vector<std::reference_wrapper<const CSG::CSGUniverse>> universe_row;
for (const auto univ_id : row)
{
const auto & univ = csg_obj->getUniverseByName(univ_id_names[univ_id]);
universe_row.push_back(univ);
}
universe_pattern.push_back(universe_row);
}
// create the lattice based on the specified type
std::string lat_name = mg_name + "_lattice";
if (_lattice_type == "cartesian")
{
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>(lat_name, _pitch, universe_pattern);
csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
}
else if (_lattice_type == "hexagonal")
{
std::unique_ptr<CSG::CSGHexagonalLattice> lat_ptr =
std::make_unique<CSG::CSGHexagonalLattice>(lat_name, _pitch, universe_pattern);
csg_obj->addLattice<CSG::CSGHexagonalLattice>(std::move(lat_ptr));
}
return csg_obj;
}
For this example, the following input would generate the corresponding JSON output below.
Example Input:
[Mesh<<<{"href": "../../syntax/Mesh/index.html"}>>>]
[sq1]
type = ExampleCSGInfiniteSquareMeshGenerator
side_length = 4
[]
[sq2]
type = ExampleCSGInfiniteSquareMeshGenerator
side_length = 3
[]
[cart_lat]
type = TestCSGLatticeMeshGenerator
lattice_type = 'cartesian'
inputs = 'sq1 sq2'
pattern = '0 0;
0 1'
pitch = 5
[]
[sq3]
type = ExampleCSGInfiniteSquareMeshGenerator
side_length = 15
fill = 'cart_lat'
[]
[]Example Output:
{
"cells": {
"sq1_square_cell": {
"fill": "square_material",
"filltype": "CSG_MATERIAL",
"region": "(+sq1_surf_plus_x & -sq1_surf_minus_x & -sq1_surf_plus_y & +sq1_surf_minus_y)"
},
"sq2_square_cell": {
"fill": "square_material",
"filltype": "CSG_MATERIAL",
"region": "(+sq2_surf_plus_x & -sq2_surf_minus_x & -sq2_surf_plus_y & +sq2_surf_minus_y)"
},
"sq3_square_cell": {
"fill": "cart_lat_lattice",
"filltype": "LATTICE",
"region": "(+sq3_surf_plus_x & -sq3_surf_minus_x & -sq3_surf_plus_y & +sq3_surf_minus_y)"
}
},
"lattices": {
"cart_lat_lattice": {
"attributes": {
"ncol": 2,
"nrow": 2,
"pitch": 5.0
},
"outertype": "VOID",
"type": "CSG::CSGCartesianLattice",
"universes": [
[
"sq1_univ",
"sq1_univ"
],
[
"sq1_univ",
"sq2_univ"
]
]
}
},
"surfaces": {
"sq1_surf_minus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": 2.0
},
"type": "CSG::CSGPlane"
},
"sq1_surf_minus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": -2.0
},
"type": "CSG::CSGPlane"
},
"sq1_surf_plus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": -2.0
},
"type": "CSG::CSGPlane"
},
"sq1_surf_plus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": 2.0
},
"type": "CSG::CSGPlane"
},
"sq2_surf_minus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": 1.5
},
"type": "CSG::CSGPlane"
},
"sq2_surf_minus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": -1.5
},
"type": "CSG::CSGPlane"
},
"sq2_surf_plus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": -1.5
},
"type": "CSG::CSGPlane"
},
"sq2_surf_plus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": 1.5
},
"type": "CSG::CSGPlane"
},
"sq3_surf_minus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": 7.5
},
"type": "CSG::CSGPlane"
},
"sq3_surf_minus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": -7.5
},
"type": "CSG::CSGPlane"
},
"sq3_surf_plus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": -7.5
},
"type": "CSG::CSGPlane"
},
"sq3_surf_plus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": 7.5
},
"type": "CSG::CSGPlane"
}
},
"universes": {
"ROOT_UNIVERSE": {
"cells": [
"sq3_square_cell"
],
"root": true
},
"sq1_univ": {
"cells": [
"sq1_square_cell"
]
},
"sq2_univ": {
"cells": [
"sq2_square_cell"
]
}
}
}
To run either of the above examples, use --allow-test-objects:
./moose_test-opt --allow-test-objects --csg-only -i tests/csg/csg_only_chained.i
./moose_test-opt --allow-test-objects --csg-only -i tests/csg/csg_lattice_cart.i
(moose/test/src/csg/TestCSGAxialSurfaceMeshGenerator.C)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "TestCSGAxialSurfaceMeshGenerator.h"
#include "MeshGenerator.h"
#include "CSGPlane.h"
registerMooseObject("MooseTestApp", TestCSGAxialSurfaceMeshGenerator);
InputParameters
TestCSGAxialSurfaceMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
// input parameter that is an existing mesh generator
params.addRequiredParam<MeshGeneratorName>("input", "The input MeshGenerator.");
// additional params for this specific mesh generator
params.addRequiredParam<Real>("axial_height", "Axial height of the model.");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
TestCSGAxialSurfaceMeshGenerator::TestCSGAxialSurfaceMeshGenerator(const InputParameters & params)
: MeshGenerator(params),
_mesh_ptr(getMesh("input")),
_axial_height(getParam<Real>("axial_height"))
{
_build_csg = &getCSGBase("input");
}
std::unique_ptr<MeshBase>
TestCSGAxialSurfaceMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
TestCSGAxialSurfaceMeshGenerator::generateCSG()
{
// get the existing CSGBase associated with the input mesh generator
// this is the CSGBase object that will be updated
std::unique_ptr<CSG::CSGBase> csg_obj = std::move(*_build_csg);
// get the names of the current mesh generator and the input mesh generator
// so that unique object naming can be enforced
auto mg_name = this->name();
auto inp_name = getParam<MeshGeneratorName>("input");
// get the expected existing cell
const auto cell_name = inp_name + "_square_cell";
const auto & csg_cell = csg_obj->getCellByName(cell_name);
// get the existing cell region to update
auto cell_region = csg_cell.getRegion();
// centroid used to determine direction for half-space
const auto centroid = Point(0, 0, 0);
// setting a default surface name purely for testing purposes
const auto default_surf_name = "default_surf";
// Add surfaces and halfspaces corresponding to top and bottom axial planes
std::vector<std::string> surf_names{"plus_z", "minus_z"};
std::vector<Real> coeffs{0.5 * _axial_height, -0.5 * _axial_height};
for (unsigned int i = 0; i < coeffs.size(); ++i)
{
// create a plane using the coefficients for the equation of a plane
// z plane equation: 0.0*x + 0.0*y + 1.0*z = (+/-)0.5 * axial_height
std::unique_ptr<CSG::CSGSurface> surface_ptr =
std::make_unique<CSG::CSGPlane>(default_surf_name, 0.0, 0.0, 1.0, coeffs[i]);
auto & csg_plane = csg_obj->addSurface(std::move(surface_ptr));
// Rename surface so that it has a unique surface name based on the mesh generator
const auto surf_name = mg_name + "_surf_" + surf_names[i];
csg_obj->renameSurface(csg_plane, surf_name);
// determine the half-space to add as an updated intersection
const auto region_direction = csg_plane.getHalfspaceFromPoint(centroid);
auto halfspace =
((region_direction == CSG::CSGSurface::Halfspace::POSITIVE) ? +csg_plane : -csg_plane);
// update the existing region with a half-space
cell_region &= halfspace;
}
// set the new region for the existing cell
csg_obj->updateCellRegion(csg_cell, cell_region);
// Rename cell as it now defines a box region instead of an infinite square region
csg_obj->renameCell(csg_cell, mg_name + "_box_cell");
return csg_obj;
}
(moose/test/src/csg/ExampleCSGInfiniteSquareMeshGenerator.C)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "ExampleCSGInfiniteSquareMeshGenerator.h"
#include "CSGBase.h"
#include "CSGPlane.h"
registerMooseObject("MooseTestApp", ExampleCSGInfiniteSquareMeshGenerator);
InputParameters
ExampleCSGInfiniteSquareMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
params.addRequiredParam<Real>("side_length", "Side length of infinite square.");
params.addParam<MeshGeneratorName>(
"fill", "optional input lattice mesh generator to fill generated cell with.");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
ExampleCSGInfiniteSquareMeshGenerator::ExampleCSGInfiniteSquareMeshGenerator(
const InputParameters & params)
: MeshGenerator(params),
_side_length(getParam<Real>("side_length")),
_input_fill_name(isParamValid("fill") ? getParam<MeshGeneratorName>("fill") : ""),
_has_fill(isParamValid("fill"))
{
if (_has_fill)
{
_input_fill_mg_ptr = &getMesh("fill");
_input_fill_csg = &getCSGBase("fill");
}
}
std::unique_ptr<MeshBase>
ExampleCSGInfiniteSquareMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
ExampleCSGInfiniteSquareMeshGenerator::generateCSG()
{
// name of the current mesh generator to use for naming generated objects
auto mg_name = this->name();
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// Add surfaces and halfspaces corresponding to 4 planes of infinite square
std::vector<std::vector<Point>> points_on_planes{{Point(1. * _side_length / 2., 0., 0.),
Point(1. * _side_length / 2., 1., 0.),
Point(1. * _side_length / 2., 0., 1.)},
{Point(-1. * _side_length / 2., 0., 0.),
Point(-1. * _side_length / 2., 1., 0.),
Point(-1. * _side_length / 2., 0., 1.)},
{Point(0., 1. * _side_length / 2., 0.),
Point(1., 1. * _side_length / 2., 0.),
Point(0., 1. * _side_length / 2., 1.)},
{Point(0., -1. * _side_length / 2., 0.),
Point(1., -1. * _side_length / 2., 0.),
Point(0., -1. * _side_length / 2., 1.)}};
std::vector<std::string> surf_names{"plus_x", "minus_x", "plus_y", "minus_y"};
// initialize cell region to be updated
CSG::CSGRegion region;
// set the center of the prism to be used for determining half-spaces
const auto centroid = Point(0, 0, 0);
for (unsigned int i = 0; i < points_on_planes.size(); ++i)
{
// object name includes the mesh generator name for uniqueness
const auto surf_name = mg_name + "_surf_" + surf_names[i];
// create the plane for one face of the prism
std::unique_ptr<CSG::CSGSurface> plane_ptr = std::make_unique<CSG::CSGPlane>(
surf_name, points_on_planes[i][0], points_on_planes[i][1], points_on_planes[i][2]);
auto & csg_plane = csg_obj->addSurface(std::move(plane_ptr));
// determine where the plane is in relation to the centroid to be able to set the half-space
const auto region_direction = csg_plane.getHalfspaceFromPoint(centroid);
// half-space is either positive (+plane_ptr) or negative (-plane_ptr)
// depending on the direction to the centroid
auto halfspace =
((region_direction == CSG::CSGSurface::Halfspace::POSITIVE) ? +csg_plane : -csg_plane);
// check if this is the first half-space to be added to the region,
// if not, update the existing region with the intersection of the regions (&=)
if (region.getRegionType() == CSG::CSGRegion::RegionType::EMPTY)
region = halfspace;
else
region &= halfspace;
}
// create the cell defined by the surfaces and region just created
const auto cell_name = mg_name + "_square_cell";
// determine fill: either from input fill mesh generator or default material
if (_has_fill)
{
// join the fill CSGBase into the current CSGBase & use the lattice as the fill
csg_obj->joinOtherBase(std::move(*_input_fill_csg));
// assume input MG is a lattice type for sake of this example/test
const CSG::CSGLattice & lattice = csg_obj->getLatticeByName(_input_fill_name + "_lattice");
csg_obj->createCell(cell_name, lattice, region);
}
else // default material fill
{
const auto material_name = "square_material";
csg_obj->createCell(cell_name, material_name, region);
}
return csg_obj;
}
(moose/test/src/csg/TestCSGAxialSurfaceMeshGenerator.C)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "TestCSGAxialSurfaceMeshGenerator.h"
#include "MeshGenerator.h"
#include "CSGPlane.h"
registerMooseObject("MooseTestApp", TestCSGAxialSurfaceMeshGenerator);
InputParameters
TestCSGAxialSurfaceMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
// input parameter that is an existing mesh generator
params.addRequiredParam<MeshGeneratorName>("input", "The input MeshGenerator.");
// additional params for this specific mesh generator
params.addRequiredParam<Real>("axial_height", "Axial height of the model.");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
TestCSGAxialSurfaceMeshGenerator::TestCSGAxialSurfaceMeshGenerator(const InputParameters & params)
: MeshGenerator(params),
_mesh_ptr(getMesh("input")),
_axial_height(getParam<Real>("axial_height"))
{
_build_csg = &getCSGBase("input");
}
std::unique_ptr<MeshBase>
TestCSGAxialSurfaceMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
TestCSGAxialSurfaceMeshGenerator::generateCSG()
{
// get the existing CSGBase associated with the input mesh generator
// this is the CSGBase object that will be updated
std::unique_ptr<CSG::CSGBase> csg_obj = std::move(*_build_csg);
// get the names of the current mesh generator and the input mesh generator
// so that unique object naming can be enforced
auto mg_name = this->name();
auto inp_name = getParam<MeshGeneratorName>("input");
// get the expected existing cell
const auto cell_name = inp_name + "_square_cell";
const auto & csg_cell = csg_obj->getCellByName(cell_name);
// get the existing cell region to update
auto cell_region = csg_cell.getRegion();
// centroid used to determine direction for half-space
const auto centroid = Point(0, 0, 0);
// setting a default surface name purely for testing purposes
const auto default_surf_name = "default_surf";
// Add surfaces and halfspaces corresponding to top and bottom axial planes
std::vector<std::string> surf_names{"plus_z", "minus_z"};
std::vector<Real> coeffs{0.5 * _axial_height, -0.5 * _axial_height};
for (unsigned int i = 0; i < coeffs.size(); ++i)
{
// create a plane using the coefficients for the equation of a plane
// z plane equation: 0.0*x + 0.0*y + 1.0*z = (+/-)0.5 * axial_height
std::unique_ptr<CSG::CSGSurface> surface_ptr =
std::make_unique<CSG::CSGPlane>(default_surf_name, 0.0, 0.0, 1.0, coeffs[i]);
auto & csg_plane = csg_obj->addSurface(std::move(surface_ptr));
// Rename surface so that it has a unique surface name based on the mesh generator
const auto surf_name = mg_name + "_surf_" + surf_names[i];
csg_obj->renameSurface(csg_plane, surf_name);
// determine the half-space to add as an updated intersection
const auto region_direction = csg_plane.getHalfspaceFromPoint(centroid);
auto halfspace =
((region_direction == CSG::CSGSurface::Halfspace::POSITIVE) ? +csg_plane : -csg_plane);
// update the existing region with a half-space
cell_region &= halfspace;
}
// set the new region for the existing cell
csg_obj->updateCellRegion(csg_cell, cell_region);
// Rename cell as it now defines a box region instead of an infinite square region
csg_obj->renameCell(csg_cell, mg_name + "_box_cell");
return csg_obj;
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/test/src/csg/TestCSGLatticeMeshGenerator.C)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "TestCSGLatticeMeshGenerator.h"
#include "MeshGenerator.h"
#include "CSGPlane.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
registerMooseObject("MooseTestApp", TestCSGLatticeMeshGenerator);
InputParameters
TestCSGLatticeMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
// input parameter that is an existing mesh generator
params.addRequiredParam<std::vector<MeshGeneratorName>>(
"inputs",
"The MeshGenerators that form the components of the lattice. Order of inputs corresponds to "
"the associated integer ID for the pattern (i.e., 0 for first input, 1 for second input, "
"etc.)");
params.addRequiredParam<std::string>(
"lattice_type", "The type of lattice to create. Options are 'cartesian' and 'hexagonal'.");
params.addRequiredParam<Real>("pitch",
"The pitch (flat-to-flat distance) of each lattice element.");
params.addRequiredParam<std::vector<std::vector<unsigned int>>>(
"pattern",
"A double-indexed array starting with the upper-left corner where the index"
"represents the index of the mesh/CSG generator in the 'inputs' vector");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
TestCSGLatticeMeshGenerator::TestCSGLatticeMeshGenerator(const InputParameters & params)
: MeshGenerator(params),
_lattice_type(getParam<std::string>("lattice_type")),
_pitch(getParam<Real>("pitch")),
_input_names(getParam<std::vector<MeshGeneratorName>>("inputs")),
_mesh_ptrs(getMeshes("inputs")),
_pattern(getParam<std::vector<std::vector<unsigned int>>>("pattern"))
{
for (auto inp : _input_names)
_input_csgs.push_back(&getCSGBaseByName(inp));
}
std::unique_ptr<MeshBase>
TestCSGLatticeMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
TestCSGLatticeMeshGenerator::generateCSG()
{
// create a new CSGBase object to build the lattice in
auto csg_obj = std::make_unique<CSG::CSGBase>();
// get the name of the current mesh generator
auto mg_name = this->name();
// join each input CSGBase into the new CSGBase as a unique universe
std::unordered_map<unsigned int, std::string> univ_id_names;
for (const auto i : index_range(_input_names))
{
std::string join_name = _input_names[i] + "_univ";
csg_obj->joinOtherBase(std::move(*_input_csgs[i]), join_name);
univ_id_names[i] = join_name;
}
// build the universe pattern for the lattice using the input pattern
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> universe_pattern;
for (const auto & row : _pattern)
{
std::vector<std::reference_wrapper<const CSG::CSGUniverse>> universe_row;
for (const auto univ_id : row)
{
const auto & univ = csg_obj->getUniverseByName(univ_id_names[univ_id]);
universe_row.push_back(univ);
}
universe_pattern.push_back(universe_row);
}
// create the lattice based on the specified type
std::string lat_name = mg_name + "_lattice";
if (_lattice_type == "cartesian")
{
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>(lat_name, _pitch, universe_pattern);
csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
}
else if (_lattice_type == "hexagonal")
{
std::unique_ptr<CSG::CSGHexagonalLattice> lat_ptr =
std::make_unique<CSG::CSGHexagonalLattice>(lat_name, _pitch, universe_pattern);
csg_obj->addLattice<CSG::CSGHexagonalLattice>(std::move(lat_ptr));
}
return csg_obj;
}
(moose/unit/src/CSGLatticeTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "CSGUniverse.h"
#include "CSGCell.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGLattice class and derived classes
*/
/// tests valid CSGCartesianLattice construction
TEST(CSGLatticeTest, testCreateCartLatticeValid)
{
// universe map and outer universe to use throughout tests
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
const auto outer_univ = CSGUniverse("outer_univ", false);
{
// initialize without universe map, outer is void, and pitch=1.0
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
// check dimensions/attributes
ASSERT_EQ(cart_lattice.getNRows(), 0);
ASSERT_EQ(cart_lattice.getNCols(), 0);
ASSERT_EQ(cart_lattice.getPitch(), 1.0);
// expect no universe map to be present yet
ASSERT_EQ(cart_lattice.getUniverses().size(), 0);
// check other attributes
ASSERT_TRUE(cart_lattice.getName() == "cartlat");
ASSERT_TRUE(cart_lattice.getType() == "CSG::CSGCartesianLattice");
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
}
{
// initialize with an array of universes, pitch=1.0
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
// check dimensions/attributes
ASSERT_EQ(cart_lattice.getNRows(), 2);
ASSERT_EQ(cart_lattice.getNCols(), 3);
ASSERT_EQ(cart_lattice.getPitch(), 1.0);
// expect 2x3 array
ASSERT_EQ(cart_lattice.getUniverses().size(), 2);
ASSERT_EQ(cart_lattice.getUniverses()[0].size(), 3);
ASSERT_EQ(cart_lattice.getUniverses()[1].size(), 3);
// check other attributes
ASSERT_TRUE(cart_lattice.getName() == "cartlat");
ASSERT_TRUE(cart_lattice.getType() == "CSG::CSGCartesianLattice");
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
}
{
// initialize without universe map but set outer universe
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, outer_univ);
ASSERT_EQ(cart_lattice.getOuterType(), "UNIVERSE");
ASSERT_EQ(cart_lattice.getOuterUniverse(), outer_univ);
}
{
// initialize with universe map and set outer fill to be a universe
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map, outer_univ);
ASSERT_EQ(cart_lattice.getOuterType(), "UNIVERSE");
ASSERT_EQ(cart_lattice.getOuterUniverse(), outer_univ);
}
{
// initialize without universe map but set outer to a material
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, "outer_mat");
ASSERT_EQ(cart_lattice.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(cart_lattice.getOuterMaterial(), "outer_mat");
}
{
// initialize with universe map but set outer material
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map, "outer_mat");
ASSERT_EQ(cart_lattice.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(cart_lattice.getOuterMaterial(), "outer_mat");
}
}
/// tests invalid CSGCartesianLattice construction
TEST(CSGLatticeTest, testCreateCartLatticeInvalid)
{
{
// try initialize with invalid dimension for pitch
Moose::UnitUtils::assertThrows(
[]() { CSGCartesianLattice("cartlat", -1.0); },
"Lattice cartlat must have pitch greater than 0."); // invalid pitch
}
{
// try to initialize with universe array of invalid dimensions (second row is different length)
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1}};
std::string exp_msg = "Cannot set lattice cartlat with universes. Does not have valid "
"dimensions for lattice type CSG::CSGCartesianLattice";
Moose::UnitUtils::assertThrows([&univ_map]() { CSGCartesianLattice("cartlat", 1.0, univ_map); },
exp_msg);
}
}
/// tests valid CSGHexagonalLattice construction
TEST(CSGLatticeTest, testCreateHexLatticeValid)
{
// universe map and outer universe to use throughout tests
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
const auto outer_univ = CSGUniverse("outer_univ", false);
{
// initialize without universes: pitch=1.0
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0);
// check dimensions and properties
ASSERT_EQ(hex_lat.getNRows(), 0);
ASSERT_EQ(hex_lat.getNRings(), 0);
ASSERT_EQ(hex_lat.getPitch(), 1.0);
ASSERT_EQ(hex_lat.getUniverses().size(), 0); // no universe map yet
ASSERT_TRUE(hex_lat.getName() == "hexlat");
ASSERT_TRUE(hex_lat.getType() == "CSG::CSGHexagonalLattice");
ASSERT_EQ(hex_lat.getOuterType(), "VOID");
}
{
// initialize with universe map, pitch=1.0
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, univ_map);
ASSERT_EQ(hex_lat.getNRings(), 3);
ASSERT_EQ(hex_lat.getPitch(), 1.0);
ASSERT_EQ(hex_lat.getNRows(), 5); // should be 2*nring -1 (auto calculated)
ASSERT_EQ(hex_lat.getUniverses().size(), 5);
ASSERT_EQ(hex_lat.getUniverses()[0].size(), 3);
ASSERT_EQ(hex_lat.getUniverses()[1].size(), 4);
ASSERT_EQ(hex_lat.getUniverses()[2].size(), 5);
ASSERT_EQ(hex_lat.getUniverses()[3].size(), 4);
ASSERT_EQ(hex_lat.getUniverses()[4].size(), 3);
ASSERT_TRUE(hex_lat.getName() == "hexlat");
ASSERT_TRUE(hex_lat.getType() == "CSG::CSGHexagonalLattice");
ASSERT_EQ(hex_lat.getOuterType(), "VOID");
}
{
// initialize without universe map but set outer universe
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, outer_univ);
ASSERT_EQ(hex_lat.getOuterType(), "UNIVERSE");
ASSERT_EQ(hex_lat.getOuterUniverse(), outer_univ);
}
{
// initialize with universe map but set outer universe
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, univ_map, outer_univ);
ASSERT_EQ(hex_lat.getOuterType(), "UNIVERSE");
ASSERT_EQ(hex_lat.getOuterUniverse(), outer_univ);
}
{
// initialize without universe map but set outer material
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, "outer_mat");
ASSERT_EQ(hex_lat.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(hex_lat.getOuterMaterial(), "outer_mat");
}
{
// initialize with universe map but set outer material
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, univ_map, "outer_mat");
ASSERT_EQ(hex_lat.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(hex_lat.getOuterMaterial(), "outer_mat");
}
}
/// tests invalid CSGHexagonalLattice construction
TEST(CSGLatticeTest, testCreateHexLatticeInvalid)
{
const auto univ1 = CSGUniverse("univ1", false);
{
// try initialize empty by providing invalid dimensions
Moose::UnitUtils::assertThrows(
[]() { CSGHexagonalLattice("hexlat", -1.0); },
"Lattice hexlat must have pitch greater than 0."); // invalid pitch
}
{
// create universe map with invalid dimensions (even number of rows)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
std::string exp_msg = "Cannot set lattice hexlat with universes. Does not have valid "
"dimensions for lattice type CSG::CSGHexagonalLattice";
Moose::UnitUtils::assertThrows([&univ_map]() { CSGHexagonalLattice("hexlat", 1.0, univ_map); },
exp_msg);
}
{
// create universe map with invalid dimensions (one row has wrong number of elements)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1}, // should have 5 elements
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
std::string exp_msg = "Cannot set lattice hexlat with universes. Does not have valid "
"dimensions for lattice type CSG::CSGHexagonalLattice";
Moose::UnitUtils::assertThrows([&univ_map]() { CSGHexagonalLattice("hexlat", 1.0, univ_map); },
exp_msg);
}
}
/// tests getAttributes function for both CSGCartesianLattice and CSGHexagonalLattice
TEST(CSGLatticeTest, testGetAttributes)
{
const auto univ1 = CSGUniverse("univ1", false);
{
// cartesian lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
auto dims_map = cart_lattice.getAttributes();
ASSERT_EQ(std::get<unsigned int>(dims_map["nrow"]), 2);
ASSERT_EQ(std::get<unsigned int>(dims_map["ncol"]), 3);
ASSERT_EQ(std::get<Real>(dims_map["pitch"]), 1.0);
}
{
// hexagonal lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
auto hex_lattice = CSGHexagonalLattice("hexlat", 1.0, univ_map);
auto dims_map = hex_lattice.getAttributes();
ASSERT_EQ(std::get<unsigned int>(dims_map["nrow"]), 3);
ASSERT_EQ(std::get<unsigned int>(dims_map["nring"]), 2); // should be (nrow + 1)/2
ASSERT_EQ(std::get<Real>(dims_map["pitch"]), 1.0);
}
}
/// tests CSGCartesianLattice::setUniverses function
TEST(CSGLatticeTest, testCartSetUniverses)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
// create initial lattice without a map
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
{
// create universe map and set it on the initialized lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
ASSERT_NO_THROW(cart_lattice.setUniverses(univ_map));
// should have 1x4 map after being set
ASSERT_EQ(cart_lattice.getUniverses().size(), 2);
ASSERT_EQ(cart_lattice.getUniverses()[0].size(), 3);
ASSERT_EQ(cart_lattice.getUniverses()[1].size(), 3);
// make sure dimensions were updated
ASSERT_EQ(cart_lattice.getNRows(), 2);
ASSERT_EQ(cart_lattice.getNCols(), 3);
}
{
// overwrite w/ new universe map of different dimensions - valid
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univ_map = {
{univ2, univ2, univ2, univ2}};
ASSERT_NO_THROW(cart_lattice.setUniverses(new_univ_map));
// expect map to contain all univ2
for (auto univ_list : cart_lattice.getUniverses())
{
for (const CSGUniverse & univ : univ_list)
ASSERT_EQ(univ, univ2);
}
// should have 1x4 map after being set
ASSERT_EQ(cart_lattice.getUniverses().size(), 1);
ASSERT_EQ(cart_lattice.getUniverses()[0].size(), 4);
// make sure dimensions were updated
ASSERT_EQ(cart_lattice.getNRows(), 1);
ASSERT_EQ(cart_lattice.getNCols(), 4);
}
}
/// tests CSGHexagonalLattice::setUniverses function
TEST(CSGLatticeTest, testHexSetUniverses)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
// initial empty lattice
auto lat = CSGHexagonalLattice("lat", 1.0);
{
// create universe map and then set it on the initialized lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
ASSERT_NO_THROW(lat.setUniverses(univ_map););
// should have a 2-ring map (3 rows) after being set
ASSERT_EQ(lat.getUniverses().size(), 3);
ASSERT_EQ(lat.getUniverses()[0].size(), 2);
ASSERT_EQ(lat.getUniverses()[1].size(), 3);
ASSERT_EQ(lat.getUniverses()[2].size(), 2);
// make sure dimensions were set
ASSERT_EQ(lat.getNRows(), 3);
}
{
// create new map with new dimensions and update lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univ_map = {
{univ2, univ2, univ2},
{univ2, univ2, univ2, univ2},
{univ2, univ2, univ2, univ2, univ2},
{univ2, univ2, univ2, univ2},
{univ2, univ2, univ2}};
lat.setUniverses(new_univ_map);
// expect map to contain all univ2
for (auto univ_list : lat.getUniverses())
{
for (const CSGUniverse & univ : univ_list)
ASSERT_EQ(univ, univ2);
}
// should have 3-ring (5 row) map after being set
ASSERT_EQ(lat.getUniverses().size(), 5);
ASSERT_EQ(lat.getUniverses()[0].size(), 3);
ASSERT_EQ(lat.getUniverses()[1].size(), 4);
ASSERT_EQ(lat.getUniverses()[2].size(), 5);
ASSERT_EQ(lat.getUniverses()[3].size(), 4);
ASSERT_EQ(lat.getUniverses()[4].size(), 3);
// make sure dimensions were updated
ASSERT_EQ(lat.getNRows(), 5);
}
}
/// tests CSGLattice::getUniverseNameMap function
TEST(CSGLatticeTest, testGetUniverseNameMap)
{
std::string name1 = "pinky";
std::string name2 = "brain";
const auto univ1 = CSGUniverse(name1, false);
const auto univ2 = CSGUniverse(name2, false);
// create cartesian lattice with 2x2 universe map
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ2},
{univ2, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
auto name_map = cart_lattice.getUniverseNameMap();
ASSERT_EQ(name_map.size(), 2);
ASSERT_EQ(name_map[0].size(), 2);
ASSERT_EQ(name_map[1].size(), 2);
ASSERT_EQ(name_map[0][0], name1);
ASSERT_EQ(name_map[0][1], name2);
ASSERT_EQ(name_map[1][0], name2);
ASSERT_EQ(name_map[1][1], name1);
}
/// tests CSGLattice::hasUniverse function
TEST(CSGLatticeTest, testHasUniverse)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ2}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
// check for existing universes
ASSERT_TRUE(cart_lattice.hasUniverse("univ1"));
ASSERT_TRUE(cart_lattice.hasUniverse("univ2"));
// check for non-existing universe
ASSERT_FALSE(cart_lattice.hasUniverse("univ3"));
}
/// tests CSGCartesianLattice::isValidIndex function
TEST(CSGLatticeTest, testCartIsValidIndex)
{
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
{
// test valid index locations
ASSERT_TRUE(cart_lattice.isValidIndex(std::make_pair(0, 0)));
ASSERT_TRUE(cart_lattice.isValidIndex(std::make_pair(1, 2)));
}
{
// test invalid index locations
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(2, 0))); // row out of bounds
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(0, 3))); // col out of bounds
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(-1, 0))); // negative row
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(0, -1))); // negative col
}
}
/// tests CSGHexagonalLattice::isValidIndex function
TEST(CSGLatticeTest, testHexIsValidIndex)
{
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
auto hex_lattice = CSGHexagonalLattice("hexlat", 1.0, univ_map);
{
// valid list of indices for 2-ring hex lattice:
std::vector<std::pair<int, int>> valid_indices = {std::make_pair(0, 0),
std::make_pair(0, 1),
std::make_pair(1, 0),
std::make_pair(1, 1),
std::make_pair(1, 2),
std::make_pair(2, 0),
std::make_pair(2, 1)};
// check that all valid indices return true
for (const auto & index : valid_indices)
ASSERT_TRUE(hex_lattice.isValidIndex(index));
}
{
// check invalid for each case is caught
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(0, 2))); // col out of bounds (row 0)
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(1, 3))); // col out of bounds (row 1)
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(3, 0))); // row out of bounds
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(-1, 0))); // negative row
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(0, -1))); // negative col
}
}
/// tests CSGCartesianLattice::setUniverseAtIndex function
TEST(CSGLatticeTest, testCartSetUniverseAtIndex)
{
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
// initial map should contain structure matching univ_map (all univ1)
for (auto univ_list : cart_lattice.getUniverses())
{
for (const CSGUniverse & univ : univ_list)
ASSERT_EQ(univ, univ1);
}
{
// replace element in universe map with another using setUniverseAtIndex (valid index location)
cart_lattice.setUniverseAtIndex(univ2, std::make_pair(1, 2));
auto univs = cart_lattice.getUniverses();
for (auto i : index_range(univs))
{
for (auto j : index_range(univs[i]))
{
// all universes should be univ1 except (1, 2) location
const CSGUniverse & univ = univs[i][j];
if (i == 1 && j == 2)
ASSERT_EQ(univ, univ2);
else
ASSERT_EQ(univ, univ1);
}
}
}
{
// try replacing element at an invalid index - should raise error
Moose::UnitUtils::assertThrows(
[&cart_lattice, &univ2]() { cart_lattice.setUniverseAtIndex(univ2, std::make_pair(3, 3)); },
"Cannot set universe at location (3, 3) for lattice cartlat. Not a valid location.");
}
{
// create a lattice without any map initialized yet and try setting just one element
// should raise error about map not being initialized yet
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
Moose::UnitUtils::assertThrows(
[&cart_lattice, &univ2]() { cart_lattice.setUniverseAtIndex(univ2, std::make_pair(0, 0)); },
"Cannot set universe at location (0, 0) for lattice cartlat. "
"Universe map has not been initialized.");
}
}
/// tests CSGCartesianLattice different methods for retrieving universes or locations of universes
TEST(CSGLatticeTest, testGetMethods)
{
// test get all and get by name (valid and invalid) and get at index (valid and invalid)
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ2, univ1}, {univ2, univ1, univ2}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
{
// get universe indices by name - valid name
auto loc_list = cart_lattice.getUniverseIndices("univ1");
std::vector<std::pair<unsigned int, unsigned int>> exp_locs = {
std::make_pair(0, 0), std::make_pair(0, 2), std::make_pair(1, 1)};
ASSERT_EQ(loc_list, exp_locs);
}
{
// get universe indices by name - invalid name; should raise error
Moose::UnitUtils::assertThrows([&cart_lattice]()
{ cart_lattice.getUniverseIndices("fake_name"); },
"Universe fake_name does not exist in lattice");
}
{
// get universe at index - valid index
const CSGUniverse & retr_univ = cart_lattice.getUniverseAtIndex(std::make_pair(0, 1));
ASSERT_EQ(retr_univ, univ2);
}
{
// get universe at index - invalid index; should raise error
Moose::UnitUtils::assertThrows([&cart_lattice]()
{ cart_lattice.getUniverseAtIndex(std::make_pair(3, 3)); },
"Index (3, 3) is not a valid index for lattice ");
}
}
/// test setName functionality
TEST(CSGLatticeTest, testSetName)
{
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
cart_lattice.setName("new_name");
ASSERT_EQ(cart_lattice.getName(), "new_name");
}
/// test the == and != overloaded operators for cartesian lattices
TEST(CSGLatticeTest, testCartLatticeEquality)
{
// universe maps to use for different lattice comparisons
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
const auto out1 = CSGUniverse("outer1", false);
const auto out2 = CSGUniverse("outer2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map1 = {{univ1, univ1},
{univ1, univ1}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map2 = {{univ2, univ2},
{univ2, univ2}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map3 = {{univ1, univ1}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map4 = {{univ1},
{univ1}};
// identical lattices
auto l1 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
auto l2 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
// lattice that differs by name only
auto l3 = CSGCartesianLattice("cartlat1", 1.0, univ_map1);
// lattice that differs by universe map items
auto l4 = CSGCartesianLattice("cartlat", 1.0, univ_map2);
// lattice that differs by pitch
auto l5 = CSGCartesianLattice("cartlat", 2.0, univ_map1);
// lattice that differs by nrow
auto l6 = CSGCartesianLattice("cartlat", 1.0, univ_map3);
// lattice that differs by ncol
auto l7 = CSGCartesianLattice("cartlat", 1.0, univ_map4);
// differs by outer type - material outer
auto l8 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l8.updateOuter("outer1");
// differs by outer type - universe outer
auto l9 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l9.updateOuter(out1);
// differs by outer object - universe outer
auto l10 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l10.updateOuter(out2);
// differs by outer name - material outer
auto l11 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l11.updateOuter("outer2");
// check equality
{
ASSERT_TRUE(l1 == l2);
}
// check inequality
{
// all lattices 2-7 should differ from each other in some way
std::vector<CSGCartesianLattice> diff_compare = {l2, l3, l4, l5, l6, l7, l8, l9, l10, l11};
for (std::size_t i = 0; i < diff_compare.size(); i++)
{
for (std::size_t j = i + 1; j < diff_compare.size(); ++j)
ASSERT_TRUE(diff_compare[i] != diff_compare[j]);
}
}
}
/// test the == and != overloaded operators for hexagonal lattices
TEST(CSGLatticeTest, testHexLatticeEquality)
{
// universe maps to use for different lattice comparisons
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map1 = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map2 = {
{univ2, univ2}, {univ2, univ2, univ2}, {univ2, univ2}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map3 = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
// identical lattices
auto l1 = CSGHexagonalLattice("hexlat", 1.0, univ_map1);
auto l2 = CSGHexagonalLattice("hexlat", 1.0, univ_map1);
// lattice that differs by name only
auto l3 = CSGHexagonalLattice("hexlat1", 1.0, univ_map1);
// lattice that differs by universe map items
auto l4 = CSGHexagonalLattice("hexlat", 1.0, univ_map2);
// lattice that differs by pitch
auto l5 = CSGHexagonalLattice("hexlat", 2.0, univ_map1);
// lattice that differs by nrow/rings
auto l6 = CSGHexagonalLattice("hexlat", 1.0, univ_map3);
// check equality
{
ASSERT_TRUE(l1 == l2);
}
// check inequality
{
// all lattices 2-6 should differ from each other in some way
std::vector<CSGHexagonalLattice> diff_compare = {l2, l3, l4, l5, l6};
for (std::size_t i = 0; i < diff_compare.size(); i++)
{
for (std::size_t j = i + 1; j < diff_compare.size(); ++j)
ASSERT_TRUE(diff_compare[i] != diff_compare[j]);
}
}
}
/// test CSGLattice::getUniqueUniverses
TEST(CSGLatticeTest, testGetUniqueUniverses)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ1},
{univ2, univ1}};
auto lat = CSGCartesianLattice("cartlat", 1.0, univ_map);
auto unique = lat.getUniqueUniverses();
ASSERT_EQ(unique.size(), 2);
ASSERT_EQ(unique[0].get(), univ1);
ASSERT_EQ(unique[1].get(), univ2);
}
/// test CSG[Cartesian/Hexagonal]Lattice::setPitch
TEST(CSGLatticeTest, testSetPitch)
{
{
// cartesian lattice set pitch
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
// set valid pitch
cart_lattice.setPitch(2.5);
ASSERT_EQ(cart_lattice.getPitch(), 2.5);
// try to set invalid pitch (raise error)
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.setPitch(-0.5); },
"must have pitch greater than 0.");
}
{
// hexagonal lattice set pitch
auto hex_lat = CSGHexagonalLattice("hex_lat", 1.0);
// set valid pitch
hex_lat.setPitch(2.5);
ASSERT_EQ(hex_lat.getPitch(), 2.5);
// try to set invalid pitch (raise error)
Moose::UnitUtils::assertThrows([&hex_lat]() { hex_lat.setPitch(-0.5); },
"must have pitch greater than 0.");
}
}
/// test CSGHexagonalLattice::get[Ring/Row]IndexFrom[Row/Ring]Index
TEST(CSGLatticeTest, testHexConvertRowsRings)
{
// test that conversion between ring and row form works on 2-, 3-, and 4-ring hex lattices
const auto u = CSGUniverse("u", false);
{
// 2-ring lattice case
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> umap = {
{u, u}, {u, u, u}, {u, u}};
auto lat = CSGHexagonalLattice("lat", 1.0, umap);
std::map<std::pair<int, int>, std::pair<int, int>> exp_row_to_ring = {{{0, 0}, {0, 4}},
{{0, 1}, {0, 5}},
{{1, 0}, {0, 3}},
{{1, 1}, {1, 0}},
{{1, 2}, {0, 0}},
{{2, 0}, {0, 2}},
{{2, 1}, {0, 1}}};
for (const auto & pair : exp_row_to_ring)
{
auto row_pair = lat.getRowIndexFromRingIndex(pair.second);
ASSERT_EQ(row_pair, pair.first);
auto ring_pair = lat.getRingIndexFromRowIndex(pair.first);
ASSERT_EQ(ring_pair, pair.second);
}
// check that invalid ring index raises error
Moose::UnitUtils::assertThrows([&lat]() { lat.getRowIndexFromRingIndex(std::make_pair(2, 0)); },
"Ring 2 is not valid for hexagonal lattice lat");
Moose::UnitUtils::assertThrows([&lat]() { lat.getRowIndexFromRingIndex(std::make_pair(1, 7)); },
"Position 7 is not valid for ring 1 in hexagonal lattice lat");
// check that invalid row-column index raises error
Moose::UnitUtils::assertThrows([&lat]() { lat.getRingIndexFromRowIndex(std::make_pair(3, 0)); },
"Index (3, 0) is not a valid index for hexagonal lattice lat");
}
{
// 3-ring case
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> umap = {
{u, u, u}, {u, u, u, u}, {u, u, u, u, u}, {u, u, u, u}, {u, u, u}};
auto lat = CSGHexagonalLattice("lat", 1.0, umap);
std::map<std::pair<int, int>, std::pair<int, int>> exp_row_to_ring = {{{0, 0}, {0, 8}},
{{0, 1}, {0, 9}},
{{0, 2}, {0, 10}},
{{1, 0}, {0, 7}},
{{1, 1}, {1, 4}},
{{1, 2}, {1, 5}},
{{1, 3}, {0, 11}},
{{2, 0}, {0, 6}},
{{2, 1}, {1, 3}},
{{2, 2}, {2, 0}},
{{2, 3}, {1, 0}},
{{2, 4}, {0, 0}},
{{3, 0}, {0, 5}},
{{3, 1}, {1, 2}},
{{3, 2}, {1, 1}},
{{3, 3}, {0, 1}},
{{4, 0}, {0, 4}},
{{4, 1}, {0, 3}},
{{4, 2}, {0, 2}}};
for (const auto & pair : exp_row_to_ring)
{
auto row_pair = lat.getRowIndexFromRingIndex(pair.second);
ASSERT_EQ(row_pair, pair.first);
auto ring_pair = lat.getRingIndexFromRowIndex(pair.first);
ASSERT_EQ(ring_pair, pair.second);
}
}
{
// 4-ring case
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> umap = {
{u, u, u, u},
{u, u, u, u, u},
{u, u, u, u, u, u},
{u, u, u, u, u, u, u},
{u, u, u, u, u, u},
{u, u, u, u, u},
{u, u, u, u}};
auto lat = CSGHexagonalLattice("lat", 1.0, umap);
std::map<std::pair<int, int>, std::pair<int, int>> exp_row_to_ring = {
{{0, 0}, {0, 12}}, {{0, 1}, {0, 13}}, {{0, 2}, {0, 14}}, {{0, 3}, {0, 15}},
{{1, 0}, {0, 11}}, {{1, 1}, {1, 8}}, {{1, 2}, {1, 9}}, {{1, 3}, {1, 10}},
{{1, 4}, {0, 16}}, {{2, 0}, {0, 10}}, {{2, 1}, {1, 7}}, {{2, 2}, {2, 4}},
{{2, 3}, {2, 5}}, {{2, 4}, {1, 11}}, {{2, 5}, {0, 17}}, {{3, 0}, {0, 9}},
{{3, 1}, {1, 6}}, {{3, 2}, {2, 3}}, {{3, 3}, {3, 0}}, {{3, 4}, {2, 0}},
{{3, 5}, {1, 0}}, {{3, 6}, {0, 0}}, {{4, 0}, {0, 8}}, {{4, 1}, {1, 5}},
{{4, 2}, {2, 2}}, {{4, 3}, {2, 1}}, {{4, 4}, {1, 1}}, {{4, 5}, {0, 1}},
{{5, 0}, {0, 7}}, {{5, 1}, {1, 4}}, {{5, 2}, {1, 3}}, {{5, 3}, {1, 2}},
{{5, 4}, {0, 2}}, {{6, 0}, {0, 6}}, {{6, 1}, {0, 5}}, {{6, 2}, {0, 4}},
{{6, 3}, {0, 3}}};
for (const auto & pair : exp_row_to_ring)
{
auto row_pair = lat.getRowIndexFromRingIndex(pair.second);
ASSERT_EQ(row_pair, pair.first);
auto ring_pair = lat.getRingIndexFromRowIndex(pair.first);
ASSERT_EQ(ring_pair, pair.second);
}
}
}
/// tests that a lattice initialized without a universe map can be filled later even after it is used to fill a cell
TEST(CSGLatticeTest, testEmptyToFilled)
{
const auto univ1 = CSGUniverse("univ1", false);
{
// create lattice without any universes
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
// create cell and fill with the empty lattice
auto cell = CSGCell("cell1", &cart_lattice, CSG::CSGRegion());
// now create universe map and set it on the lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ1},
{univ1, univ1}};
ASSERT_NO_THROW(cart_lattice.setUniverses(univ_map));
// verify that the lattice in the cell has the correct universe map now
const auto & lat_in_cell = cell.getFillLattice();
ASSERT_EQ(lat_in_cell.getUniverses().size(), 2);
ASSERT_EQ(lat_in_cell.getUniverses()[0].size(), 2);
}
}
TEST(CSGLatticeTest, testUpdateOuter)
{
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
{
// check outer universe type is set to VOID by default
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
// make sure trying to get material or universe outer raises error
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterMaterial(); },
"Lattice 'cartlat' has VOID outer, not CSG_MATERIAL.");
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterUniverse(); },
"Lattice 'cartlat' has VOID outer, not UNIVERSE.");
}
{
// update outer to universe
const auto univ = CSGUniverse("univ", false);
cart_lattice.updateOuter(univ);
ASSERT_EQ(cart_lattice.getOuterType(), "UNIVERSE");
ASSERT_EQ(cart_lattice.getOuterUniverse(), univ);
// try to get material outer - should raise error because type is UNIVERSE
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterMaterial(); },
"Lattice 'cartlat' has UNIVERSE outer, not CSG_MATERIAL.");
}
{
// change outer type to a material name
cart_lattice.updateOuter("material");
ASSERT_EQ(cart_lattice.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(cart_lattice.getOuterMaterial(), "material");
// try to get universe outer - should raise error because type is CSG_MATERIAL
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterUniverse(); },
"Lattice 'cartlat' has CSG_MATERIAL outer, not UNIVERSE.");
}
{
// reset outer type - should change it back to VOID
cart_lattice.resetOuter();
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
}
}
}
(moose/unit/src/CSGLatticeTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "CSGUniverse.h"
#include "CSGCell.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGLattice class and derived classes
*/
/// tests valid CSGCartesianLattice construction
TEST(CSGLatticeTest, testCreateCartLatticeValid)
{
// universe map and outer universe to use throughout tests
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
const auto outer_univ = CSGUniverse("outer_univ", false);
{
// initialize without universe map, outer is void, and pitch=1.0
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
// check dimensions/attributes
ASSERT_EQ(cart_lattice.getNRows(), 0);
ASSERT_EQ(cart_lattice.getNCols(), 0);
ASSERT_EQ(cart_lattice.getPitch(), 1.0);
// expect no universe map to be present yet
ASSERT_EQ(cart_lattice.getUniverses().size(), 0);
// check other attributes
ASSERT_TRUE(cart_lattice.getName() == "cartlat");
ASSERT_TRUE(cart_lattice.getType() == "CSG::CSGCartesianLattice");
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
}
{
// initialize with an array of universes, pitch=1.0
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
// check dimensions/attributes
ASSERT_EQ(cart_lattice.getNRows(), 2);
ASSERT_EQ(cart_lattice.getNCols(), 3);
ASSERT_EQ(cart_lattice.getPitch(), 1.0);
// expect 2x3 array
ASSERT_EQ(cart_lattice.getUniverses().size(), 2);
ASSERT_EQ(cart_lattice.getUniverses()[0].size(), 3);
ASSERT_EQ(cart_lattice.getUniverses()[1].size(), 3);
// check other attributes
ASSERT_TRUE(cart_lattice.getName() == "cartlat");
ASSERT_TRUE(cart_lattice.getType() == "CSG::CSGCartesianLattice");
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
}
{
// initialize without universe map but set outer universe
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, outer_univ);
ASSERT_EQ(cart_lattice.getOuterType(), "UNIVERSE");
ASSERT_EQ(cart_lattice.getOuterUniverse(), outer_univ);
}
{
// initialize with universe map and set outer fill to be a universe
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map, outer_univ);
ASSERT_EQ(cart_lattice.getOuterType(), "UNIVERSE");
ASSERT_EQ(cart_lattice.getOuterUniverse(), outer_univ);
}
{
// initialize without universe map but set outer to a material
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, "outer_mat");
ASSERT_EQ(cart_lattice.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(cart_lattice.getOuterMaterial(), "outer_mat");
}
{
// initialize with universe map but set outer material
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map, "outer_mat");
ASSERT_EQ(cart_lattice.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(cart_lattice.getOuterMaterial(), "outer_mat");
}
}
/// tests invalid CSGCartesianLattice construction
TEST(CSGLatticeTest, testCreateCartLatticeInvalid)
{
{
// try initialize with invalid dimension for pitch
Moose::UnitUtils::assertThrows(
[]() { CSGCartesianLattice("cartlat", -1.0); },
"Lattice cartlat must have pitch greater than 0."); // invalid pitch
}
{
// try to initialize with universe array of invalid dimensions (second row is different length)
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1}};
std::string exp_msg = "Cannot set lattice cartlat with universes. Does not have valid "
"dimensions for lattice type CSG::CSGCartesianLattice";
Moose::UnitUtils::assertThrows([&univ_map]() { CSGCartesianLattice("cartlat", 1.0, univ_map); },
exp_msg);
}
}
/// tests valid CSGHexagonalLattice construction
TEST(CSGLatticeTest, testCreateHexLatticeValid)
{
// universe map and outer universe to use throughout tests
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
const auto outer_univ = CSGUniverse("outer_univ", false);
{
// initialize without universes: pitch=1.0
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0);
// check dimensions and properties
ASSERT_EQ(hex_lat.getNRows(), 0);
ASSERT_EQ(hex_lat.getNRings(), 0);
ASSERT_EQ(hex_lat.getPitch(), 1.0);
ASSERT_EQ(hex_lat.getUniverses().size(), 0); // no universe map yet
ASSERT_TRUE(hex_lat.getName() == "hexlat");
ASSERT_TRUE(hex_lat.getType() == "CSG::CSGHexagonalLattice");
ASSERT_EQ(hex_lat.getOuterType(), "VOID");
}
{
// initialize with universe map, pitch=1.0
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, univ_map);
ASSERT_EQ(hex_lat.getNRings(), 3);
ASSERT_EQ(hex_lat.getPitch(), 1.0);
ASSERT_EQ(hex_lat.getNRows(), 5); // should be 2*nring -1 (auto calculated)
ASSERT_EQ(hex_lat.getUniverses().size(), 5);
ASSERT_EQ(hex_lat.getUniverses()[0].size(), 3);
ASSERT_EQ(hex_lat.getUniverses()[1].size(), 4);
ASSERT_EQ(hex_lat.getUniverses()[2].size(), 5);
ASSERT_EQ(hex_lat.getUniverses()[3].size(), 4);
ASSERT_EQ(hex_lat.getUniverses()[4].size(), 3);
ASSERT_TRUE(hex_lat.getName() == "hexlat");
ASSERT_TRUE(hex_lat.getType() == "CSG::CSGHexagonalLattice");
ASSERT_EQ(hex_lat.getOuterType(), "VOID");
}
{
// initialize without universe map but set outer universe
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, outer_univ);
ASSERT_EQ(hex_lat.getOuterType(), "UNIVERSE");
ASSERT_EQ(hex_lat.getOuterUniverse(), outer_univ);
}
{
// initialize with universe map but set outer universe
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, univ_map, outer_univ);
ASSERT_EQ(hex_lat.getOuterType(), "UNIVERSE");
ASSERT_EQ(hex_lat.getOuterUniverse(), outer_univ);
}
{
// initialize without universe map but set outer material
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, "outer_mat");
ASSERT_EQ(hex_lat.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(hex_lat.getOuterMaterial(), "outer_mat");
}
{
// initialize with universe map but set outer material
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, univ_map, "outer_mat");
ASSERT_EQ(hex_lat.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(hex_lat.getOuterMaterial(), "outer_mat");
}
}
/// tests invalid CSGHexagonalLattice construction
TEST(CSGLatticeTest, testCreateHexLatticeInvalid)
{
const auto univ1 = CSGUniverse("univ1", false);
{
// try initialize empty by providing invalid dimensions
Moose::UnitUtils::assertThrows(
[]() { CSGHexagonalLattice("hexlat", -1.0); },
"Lattice hexlat must have pitch greater than 0."); // invalid pitch
}
{
// create universe map with invalid dimensions (even number of rows)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
std::string exp_msg = "Cannot set lattice hexlat with universes. Does not have valid "
"dimensions for lattice type CSG::CSGHexagonalLattice";
Moose::UnitUtils::assertThrows([&univ_map]() { CSGHexagonalLattice("hexlat", 1.0, univ_map); },
exp_msg);
}
{
// create universe map with invalid dimensions (one row has wrong number of elements)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1}, // should have 5 elements
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
std::string exp_msg = "Cannot set lattice hexlat with universes. Does not have valid "
"dimensions for lattice type CSG::CSGHexagonalLattice";
Moose::UnitUtils::assertThrows([&univ_map]() { CSGHexagonalLattice("hexlat", 1.0, univ_map); },
exp_msg);
}
}
/// tests getAttributes function for both CSGCartesianLattice and CSGHexagonalLattice
TEST(CSGLatticeTest, testGetAttributes)
{
const auto univ1 = CSGUniverse("univ1", false);
{
// cartesian lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
auto dims_map = cart_lattice.getAttributes();
ASSERT_EQ(std::get<unsigned int>(dims_map["nrow"]), 2);
ASSERT_EQ(std::get<unsigned int>(dims_map["ncol"]), 3);
ASSERT_EQ(std::get<Real>(dims_map["pitch"]), 1.0);
}
{
// hexagonal lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
auto hex_lattice = CSGHexagonalLattice("hexlat", 1.0, univ_map);
auto dims_map = hex_lattice.getAttributes();
ASSERT_EQ(std::get<unsigned int>(dims_map["nrow"]), 3);
ASSERT_EQ(std::get<unsigned int>(dims_map["nring"]), 2); // should be (nrow + 1)/2
ASSERT_EQ(std::get<Real>(dims_map["pitch"]), 1.0);
}
}
/// tests CSGCartesianLattice::setUniverses function
TEST(CSGLatticeTest, testCartSetUniverses)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
// create initial lattice without a map
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
{
// create universe map and set it on the initialized lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
ASSERT_NO_THROW(cart_lattice.setUniverses(univ_map));
// should have 1x4 map after being set
ASSERT_EQ(cart_lattice.getUniverses().size(), 2);
ASSERT_EQ(cart_lattice.getUniverses()[0].size(), 3);
ASSERT_EQ(cart_lattice.getUniverses()[1].size(), 3);
// make sure dimensions were updated
ASSERT_EQ(cart_lattice.getNRows(), 2);
ASSERT_EQ(cart_lattice.getNCols(), 3);
}
{
// overwrite w/ new universe map of different dimensions - valid
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univ_map = {
{univ2, univ2, univ2, univ2}};
ASSERT_NO_THROW(cart_lattice.setUniverses(new_univ_map));
// expect map to contain all univ2
for (auto univ_list : cart_lattice.getUniverses())
{
for (const CSGUniverse & univ : univ_list)
ASSERT_EQ(univ, univ2);
}
// should have 1x4 map after being set
ASSERT_EQ(cart_lattice.getUniverses().size(), 1);
ASSERT_EQ(cart_lattice.getUniverses()[0].size(), 4);
// make sure dimensions were updated
ASSERT_EQ(cart_lattice.getNRows(), 1);
ASSERT_EQ(cart_lattice.getNCols(), 4);
}
}
/// tests CSGHexagonalLattice::setUniverses function
TEST(CSGLatticeTest, testHexSetUniverses)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
// initial empty lattice
auto lat = CSGHexagonalLattice("lat", 1.0);
{
// create universe map and then set it on the initialized lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
ASSERT_NO_THROW(lat.setUniverses(univ_map););
// should have a 2-ring map (3 rows) after being set
ASSERT_EQ(lat.getUniverses().size(), 3);
ASSERT_EQ(lat.getUniverses()[0].size(), 2);
ASSERT_EQ(lat.getUniverses()[1].size(), 3);
ASSERT_EQ(lat.getUniverses()[2].size(), 2);
// make sure dimensions were set
ASSERT_EQ(lat.getNRows(), 3);
}
{
// create new map with new dimensions and update lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univ_map = {
{univ2, univ2, univ2},
{univ2, univ2, univ2, univ2},
{univ2, univ2, univ2, univ2, univ2},
{univ2, univ2, univ2, univ2},
{univ2, univ2, univ2}};
lat.setUniverses(new_univ_map);
// expect map to contain all univ2
for (auto univ_list : lat.getUniverses())
{
for (const CSGUniverse & univ : univ_list)
ASSERT_EQ(univ, univ2);
}
// should have 3-ring (5 row) map after being set
ASSERT_EQ(lat.getUniverses().size(), 5);
ASSERT_EQ(lat.getUniverses()[0].size(), 3);
ASSERT_EQ(lat.getUniverses()[1].size(), 4);
ASSERT_EQ(lat.getUniverses()[2].size(), 5);
ASSERT_EQ(lat.getUniverses()[3].size(), 4);
ASSERT_EQ(lat.getUniverses()[4].size(), 3);
// make sure dimensions were updated
ASSERT_EQ(lat.getNRows(), 5);
}
}
/// tests CSGLattice::getUniverseNameMap function
TEST(CSGLatticeTest, testGetUniverseNameMap)
{
std::string name1 = "pinky";
std::string name2 = "brain";
const auto univ1 = CSGUniverse(name1, false);
const auto univ2 = CSGUniverse(name2, false);
// create cartesian lattice with 2x2 universe map
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ2},
{univ2, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
auto name_map = cart_lattice.getUniverseNameMap();
ASSERT_EQ(name_map.size(), 2);
ASSERT_EQ(name_map[0].size(), 2);
ASSERT_EQ(name_map[1].size(), 2);
ASSERT_EQ(name_map[0][0], name1);
ASSERT_EQ(name_map[0][1], name2);
ASSERT_EQ(name_map[1][0], name2);
ASSERT_EQ(name_map[1][1], name1);
}
/// tests CSGLattice::hasUniverse function
TEST(CSGLatticeTest, testHasUniverse)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ2}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
// check for existing universes
ASSERT_TRUE(cart_lattice.hasUniverse("univ1"));
ASSERT_TRUE(cart_lattice.hasUniverse("univ2"));
// check for non-existing universe
ASSERT_FALSE(cart_lattice.hasUniverse("univ3"));
}
/// tests CSGCartesianLattice::isValidIndex function
TEST(CSGLatticeTest, testCartIsValidIndex)
{
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
{
// test valid index locations
ASSERT_TRUE(cart_lattice.isValidIndex(std::make_pair(0, 0)));
ASSERT_TRUE(cart_lattice.isValidIndex(std::make_pair(1, 2)));
}
{
// test invalid index locations
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(2, 0))); // row out of bounds
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(0, 3))); // col out of bounds
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(-1, 0))); // negative row
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(0, -1))); // negative col
}
}
/// tests CSGHexagonalLattice::isValidIndex function
TEST(CSGLatticeTest, testHexIsValidIndex)
{
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
auto hex_lattice = CSGHexagonalLattice("hexlat", 1.0, univ_map);
{
// valid list of indices for 2-ring hex lattice:
std::vector<std::pair<int, int>> valid_indices = {std::make_pair(0, 0),
std::make_pair(0, 1),
std::make_pair(1, 0),
std::make_pair(1, 1),
std::make_pair(1, 2),
std::make_pair(2, 0),
std::make_pair(2, 1)};
// check that all valid indices return true
for (const auto & index : valid_indices)
ASSERT_TRUE(hex_lattice.isValidIndex(index));
}
{
// check invalid for each case is caught
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(0, 2))); // col out of bounds (row 0)
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(1, 3))); // col out of bounds (row 1)
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(3, 0))); // row out of bounds
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(-1, 0))); // negative row
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(0, -1))); // negative col
}
}
/// tests CSGCartesianLattice::setUniverseAtIndex function
TEST(CSGLatticeTest, testCartSetUniverseAtIndex)
{
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
// initial map should contain structure matching univ_map (all univ1)
for (auto univ_list : cart_lattice.getUniverses())
{
for (const CSGUniverse & univ : univ_list)
ASSERT_EQ(univ, univ1);
}
{
// replace element in universe map with another using setUniverseAtIndex (valid index location)
cart_lattice.setUniverseAtIndex(univ2, std::make_pair(1, 2));
auto univs = cart_lattice.getUniverses();
for (auto i : index_range(univs))
{
for (auto j : index_range(univs[i]))
{
// all universes should be univ1 except (1, 2) location
const CSGUniverse & univ = univs[i][j];
if (i == 1 && j == 2)
ASSERT_EQ(univ, univ2);
else
ASSERT_EQ(univ, univ1);
}
}
}
{
// try replacing element at an invalid index - should raise error
Moose::UnitUtils::assertThrows(
[&cart_lattice, &univ2]() { cart_lattice.setUniverseAtIndex(univ2, std::make_pair(3, 3)); },
"Cannot set universe at location (3, 3) for lattice cartlat. Not a valid location.");
}
{
// create a lattice without any map initialized yet and try setting just one element
// should raise error about map not being initialized yet
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
Moose::UnitUtils::assertThrows(
[&cart_lattice, &univ2]() { cart_lattice.setUniverseAtIndex(univ2, std::make_pair(0, 0)); },
"Cannot set universe at location (0, 0) for lattice cartlat. "
"Universe map has not been initialized.");
}
}
/// tests CSGCartesianLattice different methods for retrieving universes or locations of universes
TEST(CSGLatticeTest, testGetMethods)
{
// test get all and get by name (valid and invalid) and get at index (valid and invalid)
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ2, univ1}, {univ2, univ1, univ2}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
{
// get universe indices by name - valid name
auto loc_list = cart_lattice.getUniverseIndices("univ1");
std::vector<std::pair<unsigned int, unsigned int>> exp_locs = {
std::make_pair(0, 0), std::make_pair(0, 2), std::make_pair(1, 1)};
ASSERT_EQ(loc_list, exp_locs);
}
{
// get universe indices by name - invalid name; should raise error
Moose::UnitUtils::assertThrows([&cart_lattice]()
{ cart_lattice.getUniverseIndices("fake_name"); },
"Universe fake_name does not exist in lattice");
}
{
// get universe at index - valid index
const CSGUniverse & retr_univ = cart_lattice.getUniverseAtIndex(std::make_pair(0, 1));
ASSERT_EQ(retr_univ, univ2);
}
{
// get universe at index - invalid index; should raise error
Moose::UnitUtils::assertThrows([&cart_lattice]()
{ cart_lattice.getUniverseAtIndex(std::make_pair(3, 3)); },
"Index (3, 3) is not a valid index for lattice ");
}
}
/// test setName functionality
TEST(CSGLatticeTest, testSetName)
{
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
cart_lattice.setName("new_name");
ASSERT_EQ(cart_lattice.getName(), "new_name");
}
/// test the == and != overloaded operators for cartesian lattices
TEST(CSGLatticeTest, testCartLatticeEquality)
{
// universe maps to use for different lattice comparisons
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
const auto out1 = CSGUniverse("outer1", false);
const auto out2 = CSGUniverse("outer2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map1 = {{univ1, univ1},
{univ1, univ1}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map2 = {{univ2, univ2},
{univ2, univ2}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map3 = {{univ1, univ1}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map4 = {{univ1},
{univ1}};
// identical lattices
auto l1 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
auto l2 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
// lattice that differs by name only
auto l3 = CSGCartesianLattice("cartlat1", 1.0, univ_map1);
// lattice that differs by universe map items
auto l4 = CSGCartesianLattice("cartlat", 1.0, univ_map2);
// lattice that differs by pitch
auto l5 = CSGCartesianLattice("cartlat", 2.0, univ_map1);
// lattice that differs by nrow
auto l6 = CSGCartesianLattice("cartlat", 1.0, univ_map3);
// lattice that differs by ncol
auto l7 = CSGCartesianLattice("cartlat", 1.0, univ_map4);
// differs by outer type - material outer
auto l8 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l8.updateOuter("outer1");
// differs by outer type - universe outer
auto l9 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l9.updateOuter(out1);
// differs by outer object - universe outer
auto l10 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l10.updateOuter(out2);
// differs by outer name - material outer
auto l11 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l11.updateOuter("outer2");
// check equality
{
ASSERT_TRUE(l1 == l2);
}
// check inequality
{
// all lattices 2-7 should differ from each other in some way
std::vector<CSGCartesianLattice> diff_compare = {l2, l3, l4, l5, l6, l7, l8, l9, l10, l11};
for (std::size_t i = 0; i < diff_compare.size(); i++)
{
for (std::size_t j = i + 1; j < diff_compare.size(); ++j)
ASSERT_TRUE(diff_compare[i] != diff_compare[j]);
}
}
}
/// test the == and != overloaded operators for hexagonal lattices
TEST(CSGLatticeTest, testHexLatticeEquality)
{
// universe maps to use for different lattice comparisons
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map1 = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map2 = {
{univ2, univ2}, {univ2, univ2, univ2}, {univ2, univ2}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map3 = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
// identical lattices
auto l1 = CSGHexagonalLattice("hexlat", 1.0, univ_map1);
auto l2 = CSGHexagonalLattice("hexlat", 1.0, univ_map1);
// lattice that differs by name only
auto l3 = CSGHexagonalLattice("hexlat1", 1.0, univ_map1);
// lattice that differs by universe map items
auto l4 = CSGHexagonalLattice("hexlat", 1.0, univ_map2);
// lattice that differs by pitch
auto l5 = CSGHexagonalLattice("hexlat", 2.0, univ_map1);
// lattice that differs by nrow/rings
auto l6 = CSGHexagonalLattice("hexlat", 1.0, univ_map3);
// check equality
{
ASSERT_TRUE(l1 == l2);
}
// check inequality
{
// all lattices 2-6 should differ from each other in some way
std::vector<CSGHexagonalLattice> diff_compare = {l2, l3, l4, l5, l6};
for (std::size_t i = 0; i < diff_compare.size(); i++)
{
for (std::size_t j = i + 1; j < diff_compare.size(); ++j)
ASSERT_TRUE(diff_compare[i] != diff_compare[j]);
}
}
}
/// test CSGLattice::getUniqueUniverses
TEST(CSGLatticeTest, testGetUniqueUniverses)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ1},
{univ2, univ1}};
auto lat = CSGCartesianLattice("cartlat", 1.0, univ_map);
auto unique = lat.getUniqueUniverses();
ASSERT_EQ(unique.size(), 2);
ASSERT_EQ(unique[0].get(), univ1);
ASSERT_EQ(unique[1].get(), univ2);
}
/// test CSG[Cartesian/Hexagonal]Lattice::setPitch
TEST(CSGLatticeTest, testSetPitch)
{
{
// cartesian lattice set pitch
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
// set valid pitch
cart_lattice.setPitch(2.5);
ASSERT_EQ(cart_lattice.getPitch(), 2.5);
// try to set invalid pitch (raise error)
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.setPitch(-0.5); },
"must have pitch greater than 0.");
}
{
// hexagonal lattice set pitch
auto hex_lat = CSGHexagonalLattice("hex_lat", 1.0);
// set valid pitch
hex_lat.setPitch(2.5);
ASSERT_EQ(hex_lat.getPitch(), 2.5);
// try to set invalid pitch (raise error)
Moose::UnitUtils::assertThrows([&hex_lat]() { hex_lat.setPitch(-0.5); },
"must have pitch greater than 0.");
}
}
/// test CSGHexagonalLattice::get[Ring/Row]IndexFrom[Row/Ring]Index
TEST(CSGLatticeTest, testHexConvertRowsRings)
{
// test that conversion between ring and row form works on 2-, 3-, and 4-ring hex lattices
const auto u = CSGUniverse("u", false);
{
// 2-ring lattice case
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> umap = {
{u, u}, {u, u, u}, {u, u}};
auto lat = CSGHexagonalLattice("lat", 1.0, umap);
std::map<std::pair<int, int>, std::pair<int, int>> exp_row_to_ring = {{{0, 0}, {0, 4}},
{{0, 1}, {0, 5}},
{{1, 0}, {0, 3}},
{{1, 1}, {1, 0}},
{{1, 2}, {0, 0}},
{{2, 0}, {0, 2}},
{{2, 1}, {0, 1}}};
for (const auto & pair : exp_row_to_ring)
{
auto row_pair = lat.getRowIndexFromRingIndex(pair.second);
ASSERT_EQ(row_pair, pair.first);
auto ring_pair = lat.getRingIndexFromRowIndex(pair.first);
ASSERT_EQ(ring_pair, pair.second);
}
// check that invalid ring index raises error
Moose::UnitUtils::assertThrows([&lat]() { lat.getRowIndexFromRingIndex(std::make_pair(2, 0)); },
"Ring 2 is not valid for hexagonal lattice lat");
Moose::UnitUtils::assertThrows([&lat]() { lat.getRowIndexFromRingIndex(std::make_pair(1, 7)); },
"Position 7 is not valid for ring 1 in hexagonal lattice lat");
// check that invalid row-column index raises error
Moose::UnitUtils::assertThrows([&lat]() { lat.getRingIndexFromRowIndex(std::make_pair(3, 0)); },
"Index (3, 0) is not a valid index for hexagonal lattice lat");
}
{
// 3-ring case
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> umap = {
{u, u, u}, {u, u, u, u}, {u, u, u, u, u}, {u, u, u, u}, {u, u, u}};
auto lat = CSGHexagonalLattice("lat", 1.0, umap);
std::map<std::pair<int, int>, std::pair<int, int>> exp_row_to_ring = {{{0, 0}, {0, 8}},
{{0, 1}, {0, 9}},
{{0, 2}, {0, 10}},
{{1, 0}, {0, 7}},
{{1, 1}, {1, 4}},
{{1, 2}, {1, 5}},
{{1, 3}, {0, 11}},
{{2, 0}, {0, 6}},
{{2, 1}, {1, 3}},
{{2, 2}, {2, 0}},
{{2, 3}, {1, 0}},
{{2, 4}, {0, 0}},
{{3, 0}, {0, 5}},
{{3, 1}, {1, 2}},
{{3, 2}, {1, 1}},
{{3, 3}, {0, 1}},
{{4, 0}, {0, 4}},
{{4, 1}, {0, 3}},
{{4, 2}, {0, 2}}};
for (const auto & pair : exp_row_to_ring)
{
auto row_pair = lat.getRowIndexFromRingIndex(pair.second);
ASSERT_EQ(row_pair, pair.first);
auto ring_pair = lat.getRingIndexFromRowIndex(pair.first);
ASSERT_EQ(ring_pair, pair.second);
}
}
{
// 4-ring case
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> umap = {
{u, u, u, u},
{u, u, u, u, u},
{u, u, u, u, u, u},
{u, u, u, u, u, u, u},
{u, u, u, u, u, u},
{u, u, u, u, u},
{u, u, u, u}};
auto lat = CSGHexagonalLattice("lat", 1.0, umap);
std::map<std::pair<int, int>, std::pair<int, int>> exp_row_to_ring = {
{{0, 0}, {0, 12}}, {{0, 1}, {0, 13}}, {{0, 2}, {0, 14}}, {{0, 3}, {0, 15}},
{{1, 0}, {0, 11}}, {{1, 1}, {1, 8}}, {{1, 2}, {1, 9}}, {{1, 3}, {1, 10}},
{{1, 4}, {0, 16}}, {{2, 0}, {0, 10}}, {{2, 1}, {1, 7}}, {{2, 2}, {2, 4}},
{{2, 3}, {2, 5}}, {{2, 4}, {1, 11}}, {{2, 5}, {0, 17}}, {{3, 0}, {0, 9}},
{{3, 1}, {1, 6}}, {{3, 2}, {2, 3}}, {{3, 3}, {3, 0}}, {{3, 4}, {2, 0}},
{{3, 5}, {1, 0}}, {{3, 6}, {0, 0}}, {{4, 0}, {0, 8}}, {{4, 1}, {1, 5}},
{{4, 2}, {2, 2}}, {{4, 3}, {2, 1}}, {{4, 4}, {1, 1}}, {{4, 5}, {0, 1}},
{{5, 0}, {0, 7}}, {{5, 1}, {1, 4}}, {{5, 2}, {1, 3}}, {{5, 3}, {1, 2}},
{{5, 4}, {0, 2}}, {{6, 0}, {0, 6}}, {{6, 1}, {0, 5}}, {{6, 2}, {0, 4}},
{{6, 3}, {0, 3}}};
for (const auto & pair : exp_row_to_ring)
{
auto row_pair = lat.getRowIndexFromRingIndex(pair.second);
ASSERT_EQ(row_pair, pair.first);
auto ring_pair = lat.getRingIndexFromRowIndex(pair.first);
ASSERT_EQ(ring_pair, pair.second);
}
}
}
/// tests that a lattice initialized without a universe map can be filled later even after it is used to fill a cell
TEST(CSGLatticeTest, testEmptyToFilled)
{
const auto univ1 = CSGUniverse("univ1", false);
{
// create lattice without any universes
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
// create cell and fill with the empty lattice
auto cell = CSGCell("cell1", &cart_lattice, CSG::CSGRegion());
// now create universe map and set it on the lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ1},
{univ1, univ1}};
ASSERT_NO_THROW(cart_lattice.setUniverses(univ_map));
// verify that the lattice in the cell has the correct universe map now
const auto & lat_in_cell = cell.getFillLattice();
ASSERT_EQ(lat_in_cell.getUniverses().size(), 2);
ASSERT_EQ(lat_in_cell.getUniverses()[0].size(), 2);
}
}
TEST(CSGLatticeTest, testUpdateOuter)
{
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
{
// check outer universe type is set to VOID by default
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
// make sure trying to get material or universe outer raises error
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterMaterial(); },
"Lattice 'cartlat' has VOID outer, not CSG_MATERIAL.");
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterUniverse(); },
"Lattice 'cartlat' has VOID outer, not UNIVERSE.");
}
{
// update outer to universe
const auto univ = CSGUniverse("univ", false);
cart_lattice.updateOuter(univ);
ASSERT_EQ(cart_lattice.getOuterType(), "UNIVERSE");
ASSERT_EQ(cart_lattice.getOuterUniverse(), univ);
// try to get material outer - should raise error because type is UNIVERSE
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterMaterial(); },
"Lattice 'cartlat' has UNIVERSE outer, not CSG_MATERIAL.");
}
{
// change outer type to a material name
cart_lattice.updateOuter("material");
ASSERT_EQ(cart_lattice.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(cart_lattice.getOuterMaterial(), "material");
// try to get universe outer - should raise error because type is CSG_MATERIAL
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterUniverse(); },
"Lattice 'cartlat' has CSG_MATERIAL outer, not UNIVERSE.");
}
{
// reset outer type - should change it back to VOID
cart_lattice.resetOuter();
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
}
}
}
(moose/unit/src/CSGLatticeTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "CSGUniverse.h"
#include "CSGCell.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGLattice class and derived classes
*/
/// tests valid CSGCartesianLattice construction
TEST(CSGLatticeTest, testCreateCartLatticeValid)
{
// universe map and outer universe to use throughout tests
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
const auto outer_univ = CSGUniverse("outer_univ", false);
{
// initialize without universe map, outer is void, and pitch=1.0
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
// check dimensions/attributes
ASSERT_EQ(cart_lattice.getNRows(), 0);
ASSERT_EQ(cart_lattice.getNCols(), 0);
ASSERT_EQ(cart_lattice.getPitch(), 1.0);
// expect no universe map to be present yet
ASSERT_EQ(cart_lattice.getUniverses().size(), 0);
// check other attributes
ASSERT_TRUE(cart_lattice.getName() == "cartlat");
ASSERT_TRUE(cart_lattice.getType() == "CSG::CSGCartesianLattice");
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
}
{
// initialize with an array of universes, pitch=1.0
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
// check dimensions/attributes
ASSERT_EQ(cart_lattice.getNRows(), 2);
ASSERT_EQ(cart_lattice.getNCols(), 3);
ASSERT_EQ(cart_lattice.getPitch(), 1.0);
// expect 2x3 array
ASSERT_EQ(cart_lattice.getUniverses().size(), 2);
ASSERT_EQ(cart_lattice.getUniverses()[0].size(), 3);
ASSERT_EQ(cart_lattice.getUniverses()[1].size(), 3);
// check other attributes
ASSERT_TRUE(cart_lattice.getName() == "cartlat");
ASSERT_TRUE(cart_lattice.getType() == "CSG::CSGCartesianLattice");
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
}
{
// initialize without universe map but set outer universe
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, outer_univ);
ASSERT_EQ(cart_lattice.getOuterType(), "UNIVERSE");
ASSERT_EQ(cart_lattice.getOuterUniverse(), outer_univ);
}
{
// initialize with universe map and set outer fill to be a universe
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map, outer_univ);
ASSERT_EQ(cart_lattice.getOuterType(), "UNIVERSE");
ASSERT_EQ(cart_lattice.getOuterUniverse(), outer_univ);
}
{
// initialize without universe map but set outer to a material
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, "outer_mat");
ASSERT_EQ(cart_lattice.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(cart_lattice.getOuterMaterial(), "outer_mat");
}
{
// initialize with universe map but set outer material
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map, "outer_mat");
ASSERT_EQ(cart_lattice.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(cart_lattice.getOuterMaterial(), "outer_mat");
}
}
/// tests invalid CSGCartesianLattice construction
TEST(CSGLatticeTest, testCreateCartLatticeInvalid)
{
{
// try initialize with invalid dimension for pitch
Moose::UnitUtils::assertThrows(
[]() { CSGCartesianLattice("cartlat", -1.0); },
"Lattice cartlat must have pitch greater than 0."); // invalid pitch
}
{
// try to initialize with universe array of invalid dimensions (second row is different length)
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1}};
std::string exp_msg = "Cannot set lattice cartlat with universes. Does not have valid "
"dimensions for lattice type CSG::CSGCartesianLattice";
Moose::UnitUtils::assertThrows([&univ_map]() { CSGCartesianLattice("cartlat", 1.0, univ_map); },
exp_msg);
}
}
/// tests valid CSGHexagonalLattice construction
TEST(CSGLatticeTest, testCreateHexLatticeValid)
{
// universe map and outer universe to use throughout tests
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
const auto outer_univ = CSGUniverse("outer_univ", false);
{
// initialize without universes: pitch=1.0
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0);
// check dimensions and properties
ASSERT_EQ(hex_lat.getNRows(), 0);
ASSERT_EQ(hex_lat.getNRings(), 0);
ASSERT_EQ(hex_lat.getPitch(), 1.0);
ASSERT_EQ(hex_lat.getUniverses().size(), 0); // no universe map yet
ASSERT_TRUE(hex_lat.getName() == "hexlat");
ASSERT_TRUE(hex_lat.getType() == "CSG::CSGHexagonalLattice");
ASSERT_EQ(hex_lat.getOuterType(), "VOID");
}
{
// initialize with universe map, pitch=1.0
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, univ_map);
ASSERT_EQ(hex_lat.getNRings(), 3);
ASSERT_EQ(hex_lat.getPitch(), 1.0);
ASSERT_EQ(hex_lat.getNRows(), 5); // should be 2*nring -1 (auto calculated)
ASSERT_EQ(hex_lat.getUniverses().size(), 5);
ASSERT_EQ(hex_lat.getUniverses()[0].size(), 3);
ASSERT_EQ(hex_lat.getUniverses()[1].size(), 4);
ASSERT_EQ(hex_lat.getUniverses()[2].size(), 5);
ASSERT_EQ(hex_lat.getUniverses()[3].size(), 4);
ASSERT_EQ(hex_lat.getUniverses()[4].size(), 3);
ASSERT_TRUE(hex_lat.getName() == "hexlat");
ASSERT_TRUE(hex_lat.getType() == "CSG::CSGHexagonalLattice");
ASSERT_EQ(hex_lat.getOuterType(), "VOID");
}
{
// initialize without universe map but set outer universe
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, outer_univ);
ASSERT_EQ(hex_lat.getOuterType(), "UNIVERSE");
ASSERT_EQ(hex_lat.getOuterUniverse(), outer_univ);
}
{
// initialize with universe map but set outer universe
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, univ_map, outer_univ);
ASSERT_EQ(hex_lat.getOuterType(), "UNIVERSE");
ASSERT_EQ(hex_lat.getOuterUniverse(), outer_univ);
}
{
// initialize without universe map but set outer material
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, "outer_mat");
ASSERT_EQ(hex_lat.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(hex_lat.getOuterMaterial(), "outer_mat");
}
{
// initialize with universe map but set outer material
auto hex_lat = CSGHexagonalLattice("hexlat", 1.0, univ_map, "outer_mat");
ASSERT_EQ(hex_lat.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(hex_lat.getOuterMaterial(), "outer_mat");
}
}
/// tests invalid CSGHexagonalLattice construction
TEST(CSGLatticeTest, testCreateHexLatticeInvalid)
{
const auto univ1 = CSGUniverse("univ1", false);
{
// try initialize empty by providing invalid dimensions
Moose::UnitUtils::assertThrows(
[]() { CSGHexagonalLattice("hexlat", -1.0); },
"Lattice hexlat must have pitch greater than 0."); // invalid pitch
}
{
// create universe map with invalid dimensions (even number of rows)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
std::string exp_msg = "Cannot set lattice hexlat with universes. Does not have valid "
"dimensions for lattice type CSG::CSGHexagonalLattice";
Moose::UnitUtils::assertThrows([&univ_map]() { CSGHexagonalLattice("hexlat", 1.0, univ_map); },
exp_msg);
}
{
// create universe map with invalid dimensions (one row has wrong number of elements)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1}, // should have 5 elements
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
std::string exp_msg = "Cannot set lattice hexlat with universes. Does not have valid "
"dimensions for lattice type CSG::CSGHexagonalLattice";
Moose::UnitUtils::assertThrows([&univ_map]() { CSGHexagonalLattice("hexlat", 1.0, univ_map); },
exp_msg);
}
}
/// tests getAttributes function for both CSGCartesianLattice and CSGHexagonalLattice
TEST(CSGLatticeTest, testGetAttributes)
{
const auto univ1 = CSGUniverse("univ1", false);
{
// cartesian lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
auto dims_map = cart_lattice.getAttributes();
ASSERT_EQ(std::get<unsigned int>(dims_map["nrow"]), 2);
ASSERT_EQ(std::get<unsigned int>(dims_map["ncol"]), 3);
ASSERT_EQ(std::get<Real>(dims_map["pitch"]), 1.0);
}
{
// hexagonal lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
auto hex_lattice = CSGHexagonalLattice("hexlat", 1.0, univ_map);
auto dims_map = hex_lattice.getAttributes();
ASSERT_EQ(std::get<unsigned int>(dims_map["nrow"]), 3);
ASSERT_EQ(std::get<unsigned int>(dims_map["nring"]), 2); // should be (nrow + 1)/2
ASSERT_EQ(std::get<Real>(dims_map["pitch"]), 1.0);
}
}
/// tests CSGCartesianLattice::setUniverses function
TEST(CSGLatticeTest, testCartSetUniverses)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
// create initial lattice without a map
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
{
// create universe map and set it on the initialized lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
ASSERT_NO_THROW(cart_lattice.setUniverses(univ_map));
// should have 1x4 map after being set
ASSERT_EQ(cart_lattice.getUniverses().size(), 2);
ASSERT_EQ(cart_lattice.getUniverses()[0].size(), 3);
ASSERT_EQ(cart_lattice.getUniverses()[1].size(), 3);
// make sure dimensions were updated
ASSERT_EQ(cart_lattice.getNRows(), 2);
ASSERT_EQ(cart_lattice.getNCols(), 3);
}
{
// overwrite w/ new universe map of different dimensions - valid
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univ_map = {
{univ2, univ2, univ2, univ2}};
ASSERT_NO_THROW(cart_lattice.setUniverses(new_univ_map));
// expect map to contain all univ2
for (auto univ_list : cart_lattice.getUniverses())
{
for (const CSGUniverse & univ : univ_list)
ASSERT_EQ(univ, univ2);
}
// should have 1x4 map after being set
ASSERT_EQ(cart_lattice.getUniverses().size(), 1);
ASSERT_EQ(cart_lattice.getUniverses()[0].size(), 4);
// make sure dimensions were updated
ASSERT_EQ(cart_lattice.getNRows(), 1);
ASSERT_EQ(cart_lattice.getNCols(), 4);
}
}
/// tests CSGHexagonalLattice::setUniverses function
TEST(CSGLatticeTest, testHexSetUniverses)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
// initial empty lattice
auto lat = CSGHexagonalLattice("lat", 1.0);
{
// create universe map and then set it on the initialized lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
ASSERT_NO_THROW(lat.setUniverses(univ_map););
// should have a 2-ring map (3 rows) after being set
ASSERT_EQ(lat.getUniverses().size(), 3);
ASSERT_EQ(lat.getUniverses()[0].size(), 2);
ASSERT_EQ(lat.getUniverses()[1].size(), 3);
ASSERT_EQ(lat.getUniverses()[2].size(), 2);
// make sure dimensions were set
ASSERT_EQ(lat.getNRows(), 3);
}
{
// create new map with new dimensions and update lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univ_map = {
{univ2, univ2, univ2},
{univ2, univ2, univ2, univ2},
{univ2, univ2, univ2, univ2, univ2},
{univ2, univ2, univ2, univ2},
{univ2, univ2, univ2}};
lat.setUniverses(new_univ_map);
// expect map to contain all univ2
for (auto univ_list : lat.getUniverses())
{
for (const CSGUniverse & univ : univ_list)
ASSERT_EQ(univ, univ2);
}
// should have 3-ring (5 row) map after being set
ASSERT_EQ(lat.getUniverses().size(), 5);
ASSERT_EQ(lat.getUniverses()[0].size(), 3);
ASSERT_EQ(lat.getUniverses()[1].size(), 4);
ASSERT_EQ(lat.getUniverses()[2].size(), 5);
ASSERT_EQ(lat.getUniverses()[3].size(), 4);
ASSERT_EQ(lat.getUniverses()[4].size(), 3);
// make sure dimensions were updated
ASSERT_EQ(lat.getNRows(), 5);
}
}
/// tests CSGLattice::getUniverseNameMap function
TEST(CSGLatticeTest, testGetUniverseNameMap)
{
std::string name1 = "pinky";
std::string name2 = "brain";
const auto univ1 = CSGUniverse(name1, false);
const auto univ2 = CSGUniverse(name2, false);
// create cartesian lattice with 2x2 universe map
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ2},
{univ2, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
auto name_map = cart_lattice.getUniverseNameMap();
ASSERT_EQ(name_map.size(), 2);
ASSERT_EQ(name_map[0].size(), 2);
ASSERT_EQ(name_map[1].size(), 2);
ASSERT_EQ(name_map[0][0], name1);
ASSERT_EQ(name_map[0][1], name2);
ASSERT_EQ(name_map[1][0], name2);
ASSERT_EQ(name_map[1][1], name1);
}
/// tests CSGLattice::hasUniverse function
TEST(CSGLatticeTest, testHasUniverse)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ2}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
// check for existing universes
ASSERT_TRUE(cart_lattice.hasUniverse("univ1"));
ASSERT_TRUE(cart_lattice.hasUniverse("univ2"));
// check for non-existing universe
ASSERT_FALSE(cart_lattice.hasUniverse("univ3"));
}
/// tests CSGCartesianLattice::isValidIndex function
TEST(CSGLatticeTest, testCartIsValidIndex)
{
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
{
// test valid index locations
ASSERT_TRUE(cart_lattice.isValidIndex(std::make_pair(0, 0)));
ASSERT_TRUE(cart_lattice.isValidIndex(std::make_pair(1, 2)));
}
{
// test invalid index locations
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(2, 0))); // row out of bounds
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(0, 3))); // col out of bounds
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(-1, 0))); // negative row
ASSERT_FALSE(cart_lattice.isValidIndex(std::make_pair(0, -1))); // negative col
}
}
/// tests CSGHexagonalLattice::isValidIndex function
TEST(CSGLatticeTest, testHexIsValidIndex)
{
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
auto hex_lattice = CSGHexagonalLattice("hexlat", 1.0, univ_map);
{
// valid list of indices for 2-ring hex lattice:
std::vector<std::pair<int, int>> valid_indices = {std::make_pair(0, 0),
std::make_pair(0, 1),
std::make_pair(1, 0),
std::make_pair(1, 1),
std::make_pair(1, 2),
std::make_pair(2, 0),
std::make_pair(2, 1)};
// check that all valid indices return true
for (const auto & index : valid_indices)
ASSERT_TRUE(hex_lattice.isValidIndex(index));
}
{
// check invalid for each case is caught
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(0, 2))); // col out of bounds (row 0)
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(1, 3))); // col out of bounds (row 1)
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(3, 0))); // row out of bounds
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(-1, 0))); // negative row
ASSERT_FALSE(hex_lattice.isValidIndex(std::make_pair(0, -1))); // negative col
}
}
/// tests CSGCartesianLattice::setUniverseAtIndex function
TEST(CSGLatticeTest, testCartSetUniverseAtIndex)
{
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ1, univ1}, {univ1, univ1, univ1}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
// initial map should contain structure matching univ_map (all univ1)
for (auto univ_list : cart_lattice.getUniverses())
{
for (const CSGUniverse & univ : univ_list)
ASSERT_EQ(univ, univ1);
}
{
// replace element in universe map with another using setUniverseAtIndex (valid index location)
cart_lattice.setUniverseAtIndex(univ2, std::make_pair(1, 2));
auto univs = cart_lattice.getUniverses();
for (auto i : index_range(univs))
{
for (auto j : index_range(univs[i]))
{
// all universes should be univ1 except (1, 2) location
const CSGUniverse & univ = univs[i][j];
if (i == 1 && j == 2)
ASSERT_EQ(univ, univ2);
else
ASSERT_EQ(univ, univ1);
}
}
}
{
// try replacing element at an invalid index - should raise error
Moose::UnitUtils::assertThrows(
[&cart_lattice, &univ2]() { cart_lattice.setUniverseAtIndex(univ2, std::make_pair(3, 3)); },
"Cannot set universe at location (3, 3) for lattice cartlat. Not a valid location.");
}
{
// create a lattice without any map initialized yet and try setting just one element
// should raise error about map not being initialized yet
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
Moose::UnitUtils::assertThrows(
[&cart_lattice, &univ2]() { cart_lattice.setUniverseAtIndex(univ2, std::make_pair(0, 0)); },
"Cannot set universe at location (0, 0) for lattice cartlat. "
"Universe map has not been initialized.");
}
}
/// tests CSGCartesianLattice different methods for retrieving universes or locations of universes
TEST(CSGLatticeTest, testGetMethods)
{
// test get all and get by name (valid and invalid) and get at index (valid and invalid)
// create initial lattice of all univ1 elements
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {
{univ1, univ2, univ1}, {univ2, univ1, univ2}};
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0, univ_map);
{
// get universe indices by name - valid name
auto loc_list = cart_lattice.getUniverseIndices("univ1");
std::vector<std::pair<unsigned int, unsigned int>> exp_locs = {
std::make_pair(0, 0), std::make_pair(0, 2), std::make_pair(1, 1)};
ASSERT_EQ(loc_list, exp_locs);
}
{
// get universe indices by name - invalid name; should raise error
Moose::UnitUtils::assertThrows([&cart_lattice]()
{ cart_lattice.getUniverseIndices("fake_name"); },
"Universe fake_name does not exist in lattice");
}
{
// get universe at index - valid index
const CSGUniverse & retr_univ = cart_lattice.getUniverseAtIndex(std::make_pair(0, 1));
ASSERT_EQ(retr_univ, univ2);
}
{
// get universe at index - invalid index; should raise error
Moose::UnitUtils::assertThrows([&cart_lattice]()
{ cart_lattice.getUniverseAtIndex(std::make_pair(3, 3)); },
"Index (3, 3) is not a valid index for lattice ");
}
}
/// test setName functionality
TEST(CSGLatticeTest, testSetName)
{
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
cart_lattice.setName("new_name");
ASSERT_EQ(cart_lattice.getName(), "new_name");
}
/// test the == and != overloaded operators for cartesian lattices
TEST(CSGLatticeTest, testCartLatticeEquality)
{
// universe maps to use for different lattice comparisons
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
const auto out1 = CSGUniverse("outer1", false);
const auto out2 = CSGUniverse("outer2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map1 = {{univ1, univ1},
{univ1, univ1}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map2 = {{univ2, univ2},
{univ2, univ2}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map3 = {{univ1, univ1}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map4 = {{univ1},
{univ1}};
// identical lattices
auto l1 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
auto l2 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
// lattice that differs by name only
auto l3 = CSGCartesianLattice("cartlat1", 1.0, univ_map1);
// lattice that differs by universe map items
auto l4 = CSGCartesianLattice("cartlat", 1.0, univ_map2);
// lattice that differs by pitch
auto l5 = CSGCartesianLattice("cartlat", 2.0, univ_map1);
// lattice that differs by nrow
auto l6 = CSGCartesianLattice("cartlat", 1.0, univ_map3);
// lattice that differs by ncol
auto l7 = CSGCartesianLattice("cartlat", 1.0, univ_map4);
// differs by outer type - material outer
auto l8 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l8.updateOuter("outer1");
// differs by outer type - universe outer
auto l9 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l9.updateOuter(out1);
// differs by outer object - universe outer
auto l10 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l10.updateOuter(out2);
// differs by outer name - material outer
auto l11 = CSGCartesianLattice("cartlat", 1.0, univ_map1);
l11.updateOuter("outer2");
// check equality
{
ASSERT_TRUE(l1 == l2);
}
// check inequality
{
// all lattices 2-7 should differ from each other in some way
std::vector<CSGCartesianLattice> diff_compare = {l2, l3, l4, l5, l6, l7, l8, l9, l10, l11};
for (std::size_t i = 0; i < diff_compare.size(); i++)
{
for (std::size_t j = i + 1; j < diff_compare.size(); ++j)
ASSERT_TRUE(diff_compare[i] != diff_compare[j]);
}
}
}
/// test the == and != overloaded operators for hexagonal lattices
TEST(CSGLatticeTest, testHexLatticeEquality)
{
// universe maps to use for different lattice comparisons
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map1 = {
{univ1, univ1}, {univ1, univ1, univ1}, {univ1, univ1}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map2 = {
{univ2, univ2}, {univ2, univ2, univ2}, {univ2, univ2}};
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map3 = {
{univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1, univ1},
{univ1, univ1, univ1, univ1},
{univ1, univ1, univ1}};
// identical lattices
auto l1 = CSGHexagonalLattice("hexlat", 1.0, univ_map1);
auto l2 = CSGHexagonalLattice("hexlat", 1.0, univ_map1);
// lattice that differs by name only
auto l3 = CSGHexagonalLattice("hexlat1", 1.0, univ_map1);
// lattice that differs by universe map items
auto l4 = CSGHexagonalLattice("hexlat", 1.0, univ_map2);
// lattice that differs by pitch
auto l5 = CSGHexagonalLattice("hexlat", 2.0, univ_map1);
// lattice that differs by nrow/rings
auto l6 = CSGHexagonalLattice("hexlat", 1.0, univ_map3);
// check equality
{
ASSERT_TRUE(l1 == l2);
}
// check inequality
{
// all lattices 2-6 should differ from each other in some way
std::vector<CSGHexagonalLattice> diff_compare = {l2, l3, l4, l5, l6};
for (std::size_t i = 0; i < diff_compare.size(); i++)
{
for (std::size_t j = i + 1; j < diff_compare.size(); ++j)
ASSERT_TRUE(diff_compare[i] != diff_compare[j]);
}
}
}
/// test CSGLattice::getUniqueUniverses
TEST(CSGLatticeTest, testGetUniqueUniverses)
{
const auto univ1 = CSGUniverse("univ1", false);
const auto univ2 = CSGUniverse("univ2", false);
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ1},
{univ2, univ1}};
auto lat = CSGCartesianLattice("cartlat", 1.0, univ_map);
auto unique = lat.getUniqueUniverses();
ASSERT_EQ(unique.size(), 2);
ASSERT_EQ(unique[0].get(), univ1);
ASSERT_EQ(unique[1].get(), univ2);
}
/// test CSG[Cartesian/Hexagonal]Lattice::setPitch
TEST(CSGLatticeTest, testSetPitch)
{
{
// cartesian lattice set pitch
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
// set valid pitch
cart_lattice.setPitch(2.5);
ASSERT_EQ(cart_lattice.getPitch(), 2.5);
// try to set invalid pitch (raise error)
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.setPitch(-0.5); },
"must have pitch greater than 0.");
}
{
// hexagonal lattice set pitch
auto hex_lat = CSGHexagonalLattice("hex_lat", 1.0);
// set valid pitch
hex_lat.setPitch(2.5);
ASSERT_EQ(hex_lat.getPitch(), 2.5);
// try to set invalid pitch (raise error)
Moose::UnitUtils::assertThrows([&hex_lat]() { hex_lat.setPitch(-0.5); },
"must have pitch greater than 0.");
}
}
/// test CSGHexagonalLattice::get[Ring/Row]IndexFrom[Row/Ring]Index
TEST(CSGLatticeTest, testHexConvertRowsRings)
{
// test that conversion between ring and row form works on 2-, 3-, and 4-ring hex lattices
const auto u = CSGUniverse("u", false);
{
// 2-ring lattice case
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> umap = {
{u, u}, {u, u, u}, {u, u}};
auto lat = CSGHexagonalLattice("lat", 1.0, umap);
std::map<std::pair<int, int>, std::pair<int, int>> exp_row_to_ring = {{{0, 0}, {0, 4}},
{{0, 1}, {0, 5}},
{{1, 0}, {0, 3}},
{{1, 1}, {1, 0}},
{{1, 2}, {0, 0}},
{{2, 0}, {0, 2}},
{{2, 1}, {0, 1}}};
for (const auto & pair : exp_row_to_ring)
{
auto row_pair = lat.getRowIndexFromRingIndex(pair.second);
ASSERT_EQ(row_pair, pair.first);
auto ring_pair = lat.getRingIndexFromRowIndex(pair.first);
ASSERT_EQ(ring_pair, pair.second);
}
// check that invalid ring index raises error
Moose::UnitUtils::assertThrows([&lat]() { lat.getRowIndexFromRingIndex(std::make_pair(2, 0)); },
"Ring 2 is not valid for hexagonal lattice lat");
Moose::UnitUtils::assertThrows([&lat]() { lat.getRowIndexFromRingIndex(std::make_pair(1, 7)); },
"Position 7 is not valid for ring 1 in hexagonal lattice lat");
// check that invalid row-column index raises error
Moose::UnitUtils::assertThrows([&lat]() { lat.getRingIndexFromRowIndex(std::make_pair(3, 0)); },
"Index (3, 0) is not a valid index for hexagonal lattice lat");
}
{
// 3-ring case
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> umap = {
{u, u, u}, {u, u, u, u}, {u, u, u, u, u}, {u, u, u, u}, {u, u, u}};
auto lat = CSGHexagonalLattice("lat", 1.0, umap);
std::map<std::pair<int, int>, std::pair<int, int>> exp_row_to_ring = {{{0, 0}, {0, 8}},
{{0, 1}, {0, 9}},
{{0, 2}, {0, 10}},
{{1, 0}, {0, 7}},
{{1, 1}, {1, 4}},
{{1, 2}, {1, 5}},
{{1, 3}, {0, 11}},
{{2, 0}, {0, 6}},
{{2, 1}, {1, 3}},
{{2, 2}, {2, 0}},
{{2, 3}, {1, 0}},
{{2, 4}, {0, 0}},
{{3, 0}, {0, 5}},
{{3, 1}, {1, 2}},
{{3, 2}, {1, 1}},
{{3, 3}, {0, 1}},
{{4, 0}, {0, 4}},
{{4, 1}, {0, 3}},
{{4, 2}, {0, 2}}};
for (const auto & pair : exp_row_to_ring)
{
auto row_pair = lat.getRowIndexFromRingIndex(pair.second);
ASSERT_EQ(row_pair, pair.first);
auto ring_pair = lat.getRingIndexFromRowIndex(pair.first);
ASSERT_EQ(ring_pair, pair.second);
}
}
{
// 4-ring case
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> umap = {
{u, u, u, u},
{u, u, u, u, u},
{u, u, u, u, u, u},
{u, u, u, u, u, u, u},
{u, u, u, u, u, u},
{u, u, u, u, u},
{u, u, u, u}};
auto lat = CSGHexagonalLattice("lat", 1.0, umap);
std::map<std::pair<int, int>, std::pair<int, int>> exp_row_to_ring = {
{{0, 0}, {0, 12}}, {{0, 1}, {0, 13}}, {{0, 2}, {0, 14}}, {{0, 3}, {0, 15}},
{{1, 0}, {0, 11}}, {{1, 1}, {1, 8}}, {{1, 2}, {1, 9}}, {{1, 3}, {1, 10}},
{{1, 4}, {0, 16}}, {{2, 0}, {0, 10}}, {{2, 1}, {1, 7}}, {{2, 2}, {2, 4}},
{{2, 3}, {2, 5}}, {{2, 4}, {1, 11}}, {{2, 5}, {0, 17}}, {{3, 0}, {0, 9}},
{{3, 1}, {1, 6}}, {{3, 2}, {2, 3}}, {{3, 3}, {3, 0}}, {{3, 4}, {2, 0}},
{{3, 5}, {1, 0}}, {{3, 6}, {0, 0}}, {{4, 0}, {0, 8}}, {{4, 1}, {1, 5}},
{{4, 2}, {2, 2}}, {{4, 3}, {2, 1}}, {{4, 4}, {1, 1}}, {{4, 5}, {0, 1}},
{{5, 0}, {0, 7}}, {{5, 1}, {1, 4}}, {{5, 2}, {1, 3}}, {{5, 3}, {1, 2}},
{{5, 4}, {0, 2}}, {{6, 0}, {0, 6}}, {{6, 1}, {0, 5}}, {{6, 2}, {0, 4}},
{{6, 3}, {0, 3}}};
for (const auto & pair : exp_row_to_ring)
{
auto row_pair = lat.getRowIndexFromRingIndex(pair.second);
ASSERT_EQ(row_pair, pair.first);
auto ring_pair = lat.getRingIndexFromRowIndex(pair.first);
ASSERT_EQ(ring_pair, pair.second);
}
}
}
/// tests that a lattice initialized without a universe map can be filled later even after it is used to fill a cell
TEST(CSGLatticeTest, testEmptyToFilled)
{
const auto univ1 = CSGUniverse("univ1", false);
{
// create lattice without any universes
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
// create cell and fill with the empty lattice
auto cell = CSGCell("cell1", &cart_lattice, CSG::CSGRegion());
// now create universe map and set it on the lattice
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univ_map = {{univ1, univ1},
{univ1, univ1}};
ASSERT_NO_THROW(cart_lattice.setUniverses(univ_map));
// verify that the lattice in the cell has the correct universe map now
const auto & lat_in_cell = cell.getFillLattice();
ASSERT_EQ(lat_in_cell.getUniverses().size(), 2);
ASSERT_EQ(lat_in_cell.getUniverses()[0].size(), 2);
}
}
TEST(CSGLatticeTest, testUpdateOuter)
{
auto cart_lattice = CSGCartesianLattice("cartlat", 1.0);
{
// check outer universe type is set to VOID by default
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
// make sure trying to get material or universe outer raises error
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterMaterial(); },
"Lattice 'cartlat' has VOID outer, not CSG_MATERIAL.");
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterUniverse(); },
"Lattice 'cartlat' has VOID outer, not UNIVERSE.");
}
{
// update outer to universe
const auto univ = CSGUniverse("univ", false);
cart_lattice.updateOuter(univ);
ASSERT_EQ(cart_lattice.getOuterType(), "UNIVERSE");
ASSERT_EQ(cart_lattice.getOuterUniverse(), univ);
// try to get material outer - should raise error because type is UNIVERSE
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterMaterial(); },
"Lattice 'cartlat' has UNIVERSE outer, not CSG_MATERIAL.");
}
{
// change outer type to a material name
cart_lattice.updateOuter("material");
ASSERT_EQ(cart_lattice.getOuterType(), "CSG_MATERIAL");
ASSERT_EQ(cart_lattice.getOuterMaterial(), "material");
// try to get universe outer - should raise error because type is CSG_MATERIAL
Moose::UnitUtils::assertThrows([&cart_lattice]() { cart_lattice.getOuterUniverse(); },
"Lattice 'cartlat' has CSG_MATERIAL outer, not UNIVERSE.");
}
{
// reset outer type - should change it back to VOID
cart_lattice.resetOuter();
ASSERT_EQ(cart_lattice.getOuterType(), "VOID");
}
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/test/include/csg/TestCSGAxialSurfaceMeshGenerator.h)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "MeshGenerator.h"
class TestCSGAxialSurfaceMeshGenerator : public MeshGenerator
{
public:
static InputParameters validParams();
TestCSGAxialSurfaceMeshGenerator(const InputParameters & parameters);
std::unique_ptr<MeshBase> generate() override;
void generateData() override {};
std::unique_ptr<CSG::CSGBase> generateCSG() override;
protected:
/// Pointer to the input mesh
std::unique_ptr<MeshBase> & _mesh_ptr;
/// the axial height to set the input mesh to
const Real _axial_height;
/// Holds the generated CSGBase object
std::unique_ptr<CSG::CSGBase> * _build_csg;
};
(moose/test/src/csg/TestCSGAxialSurfaceMeshGenerator.C)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "TestCSGAxialSurfaceMeshGenerator.h"
#include "MeshGenerator.h"
#include "CSGPlane.h"
registerMooseObject("MooseTestApp", TestCSGAxialSurfaceMeshGenerator);
InputParameters
TestCSGAxialSurfaceMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
// input parameter that is an existing mesh generator
params.addRequiredParam<MeshGeneratorName>("input", "The input MeshGenerator.");
// additional params for this specific mesh generator
params.addRequiredParam<Real>("axial_height", "Axial height of the model.");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
TestCSGAxialSurfaceMeshGenerator::TestCSGAxialSurfaceMeshGenerator(const InputParameters & params)
: MeshGenerator(params),
_mesh_ptr(getMesh("input")),
_axial_height(getParam<Real>("axial_height"))
{
_build_csg = &getCSGBase("input");
}
std::unique_ptr<MeshBase>
TestCSGAxialSurfaceMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
TestCSGAxialSurfaceMeshGenerator::generateCSG()
{
// get the existing CSGBase associated with the input mesh generator
// this is the CSGBase object that will be updated
std::unique_ptr<CSG::CSGBase> csg_obj = std::move(*_build_csg);
// get the names of the current mesh generator and the input mesh generator
// so that unique object naming can be enforced
auto mg_name = this->name();
auto inp_name = getParam<MeshGeneratorName>("input");
// get the expected existing cell
const auto cell_name = inp_name + "_square_cell";
const auto & csg_cell = csg_obj->getCellByName(cell_name);
// get the existing cell region to update
auto cell_region = csg_cell.getRegion();
// centroid used to determine direction for half-space
const auto centroid = Point(0, 0, 0);
// setting a default surface name purely for testing purposes
const auto default_surf_name = "default_surf";
// Add surfaces and halfspaces corresponding to top and bottom axial planes
std::vector<std::string> surf_names{"plus_z", "minus_z"};
std::vector<Real> coeffs{0.5 * _axial_height, -0.5 * _axial_height};
for (unsigned int i = 0; i < coeffs.size(); ++i)
{
// create a plane using the coefficients for the equation of a plane
// z plane equation: 0.0*x + 0.0*y + 1.0*z = (+/-)0.5 * axial_height
std::unique_ptr<CSG::CSGSurface> surface_ptr =
std::make_unique<CSG::CSGPlane>(default_surf_name, 0.0, 0.0, 1.0, coeffs[i]);
auto & csg_plane = csg_obj->addSurface(std::move(surface_ptr));
// Rename surface so that it has a unique surface name based on the mesh generator
const auto surf_name = mg_name + "_surf_" + surf_names[i];
csg_obj->renameSurface(csg_plane, surf_name);
// determine the half-space to add as an updated intersection
const auto region_direction = csg_plane.getHalfspaceFromPoint(centroid);
auto halfspace =
((region_direction == CSG::CSGSurface::Halfspace::POSITIVE) ? +csg_plane : -csg_plane);
// update the existing region with a half-space
cell_region &= halfspace;
}
// set the new region for the existing cell
csg_obj->updateCellRegion(csg_cell, cell_region);
// Rename cell as it now defines a box region instead of an infinite square region
csg_obj->renameCell(csg_cell, mg_name + "_box_cell");
return csg_obj;
}
(moose/test/src/csg/TestCSGAxialSurfaceMeshGenerator.C)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "TestCSGAxialSurfaceMeshGenerator.h"
#include "MeshGenerator.h"
#include "CSGPlane.h"
registerMooseObject("MooseTestApp", TestCSGAxialSurfaceMeshGenerator);
InputParameters
TestCSGAxialSurfaceMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
// input parameter that is an existing mesh generator
params.addRequiredParam<MeshGeneratorName>("input", "The input MeshGenerator.");
// additional params for this specific mesh generator
params.addRequiredParam<Real>("axial_height", "Axial height of the model.");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
TestCSGAxialSurfaceMeshGenerator::TestCSGAxialSurfaceMeshGenerator(const InputParameters & params)
: MeshGenerator(params),
_mesh_ptr(getMesh("input")),
_axial_height(getParam<Real>("axial_height"))
{
_build_csg = &getCSGBase("input");
}
std::unique_ptr<MeshBase>
TestCSGAxialSurfaceMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
TestCSGAxialSurfaceMeshGenerator::generateCSG()
{
// get the existing CSGBase associated with the input mesh generator
// this is the CSGBase object that will be updated
std::unique_ptr<CSG::CSGBase> csg_obj = std::move(*_build_csg);
// get the names of the current mesh generator and the input mesh generator
// so that unique object naming can be enforced
auto mg_name = this->name();
auto inp_name = getParam<MeshGeneratorName>("input");
// get the expected existing cell
const auto cell_name = inp_name + "_square_cell";
const auto & csg_cell = csg_obj->getCellByName(cell_name);
// get the existing cell region to update
auto cell_region = csg_cell.getRegion();
// centroid used to determine direction for half-space
const auto centroid = Point(0, 0, 0);
// setting a default surface name purely for testing purposes
const auto default_surf_name = "default_surf";
// Add surfaces and halfspaces corresponding to top and bottom axial planes
std::vector<std::string> surf_names{"plus_z", "minus_z"};
std::vector<Real> coeffs{0.5 * _axial_height, -0.5 * _axial_height};
for (unsigned int i = 0; i < coeffs.size(); ++i)
{
// create a plane using the coefficients for the equation of a plane
// z plane equation: 0.0*x + 0.0*y + 1.0*z = (+/-)0.5 * axial_height
std::unique_ptr<CSG::CSGSurface> surface_ptr =
std::make_unique<CSG::CSGPlane>(default_surf_name, 0.0, 0.0, 1.0, coeffs[i]);
auto & csg_plane = csg_obj->addSurface(std::move(surface_ptr));
// Rename surface so that it has a unique surface name based on the mesh generator
const auto surf_name = mg_name + "_surf_" + surf_names[i];
csg_obj->renameSurface(csg_plane, surf_name);
// determine the half-space to add as an updated intersection
const auto region_direction = csg_plane.getHalfspaceFromPoint(centroid);
auto halfspace =
((region_direction == CSG::CSGSurface::Halfspace::POSITIVE) ? +csg_plane : -csg_plane);
// update the existing region with a half-space
cell_region &= halfspace;
}
// set the new region for the existing cell
csg_obj->updateCellRegion(csg_cell, cell_region);
// Rename cell as it now defines a box region instead of an infinite square region
csg_obj->renameCell(csg_cell, mg_name + "_box_cell");
return csg_obj;
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/unit/src/CSGBaseTest.C)
// This file is part of the MOOSE framework
// https://mooseframework.inl.gov
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "gtest/gtest.h"
#include "CSGBase.h"
#include "CSGSphere.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
#include "MooseUnitUtils.h"
namespace CSG
{
/**
* Tests associated with CSGSurfaceList functionality as called through CSGBase
*/
/// tests CSG[Base/SurfaceList]::addSurface() and CSG[Base/SurfaceList]::getSurfaceByName()
TEST(CSGBaseTest, testAddGetSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces that have the same name
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf", 2.0);
// add one surface to base initially
const auto & added_surf = csg_obj->addSurface(std::move(surf_ptr1));
// assert surface is present after adding by successfully using getSurfaceByName
{
// public method, returns const
ASSERT_TRUE(added_surf == csg_obj->getSurfaceByName("surf"));
// private method, returns non-const
ASSERT_TRUE(added_surf == csg_obj->getSurface("surf"));
}
// try to add surface that already exists of the same name, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj, &surf_ptr2]()
{ csg_obj->addSurface(std::move(surf_ptr2)); },
"Surface with name surf already exists in geometry.");
}
// try to get surface that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getSurfaceByName("fake_name"); },
"No surface by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/SurfaceList]::getAllSurfaces
TEST(CSGBaseTest, testGetAllSurfaces)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
csg_obj->addSurface(std::move(surf_ptr1));
csg_obj->addSurface(std::move(surf_ptr2));
auto all_surfs = csg_obj->getAllSurfaces();
ASSERT_EQ(2, all_surfs.size());
}
/// tests CSG[Base/SurfaceList]::renameSurface
TEST(CSGBaseTest, testRenameSurface)
{
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// make two surfaces to add to base
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("surf2", 2.0);
const auto & s1 = csg_obj->addSurface(std::move(surf_ptr1));
const auto & s2 = csg_obj->addSurface(std::move(surf_ptr2));
// successfully rename surface
{
csg_obj->renameSurface(s1, "george");
ASSERT_EQ("george", s1.getName());
}
// error should be raised if try to rename to a name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj, &s2]() { csg_obj->renameSurface(s2, "george"); },
"Surface with name george already exists in geometry");
}
// error should be raised if trying to rename a surface that is not a part of this instance
{
// initialize a new CSGBase object
auto csg_obj_new = std::make_unique<CSG::CSGBase>();
// make new surface to add to new base
std::unique_ptr<CSG::CSGSphere> surf_ptr3 = std::make_unique<CSG::CSGSphere>("surf3", 1.0);
const auto & s3 = csg_obj_new->addSurface(std::move(surf_ptr3));
// try to rename s3 via original base where it was not added
Moose::UnitUtils::assertThrows([&csg_obj, &s3]() { csg_obj->renameSurface(s3, "ringo"); },
"cannot be renamed to ringo as it does not exist");
}
}
/// tests CSGBase::checkRegionSurfaces
TEST(CSGBaseTest, testCheckRegionSurfaces)
{
// make two sets of surfaces that are identical but different base ownership
// create a region from surfaces in base 1 and make sure that base 2 recognizes the surfaces as
// not available in that base even though names exist
auto csg_obj1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
const auto & s1 = csg_obj1->addSurface(std::move(surf1));
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf", 1.0);
csg_obj2->addSurface(std::move(surf2));
auto reg1 = +s1; // uses surfaces from base 1
// expect error when surfaces are checked in base2
Moose::UnitUtils::assertThrows([&csg_obj2, ®1]() { csg_obj2->checkRegionSurfaces(reg1); },
"Region is being set with a surface named surf that is different "
"from the surface of the same name in the CSGBase instance.");
}
/**
* Tests associated with CSGCellList or CSGCell functionality as called through CSGBase
*/
/// tests CSG[Base/CellList]::createCell
TEST(CSGBaseTest, testCreateCell)
{
// create each type of cell, each w/ or w/out add_to_univ specified to test universe ownership
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// surfaces for regions for cell
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto reg1 = +s1;
// make a new universe to which the new cells can be added at time of creation
auto & add_to_univ = csg_obj->createUniverse("add_univ");
// root universe to check in tests
auto & root_univ = csg_obj->getRootUniverse();
// create lattice to be used as fill
auto & lat_univ1 = csg_obj->createUniverse("latt_univ1");
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr = std::make_unique<CSG::CSGCartesianLattice>(
"lat1",
1.0,
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>>{
{std::cref(lat_univ1), std::cref(lat_univ1)}});
const auto & lattice = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// make void cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "void_cell1";
// create a void cell with name cname1 and defined by region reg1
csg_obj->createCell(cname1, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "void_cell2";
csg_obj->createCell(cname2, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make material cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "mat_cell1";
// create a material-filled cell with name cname1, a fill with material matname,
// and defined by region reg1
csg_obj->createCell(cname1, "matname", reg1);
// create a cell and add to different universe, not root
std::string cname2 = "mat_cell2";
csg_obj->createCell(cname2, "matname", reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// make universe cells and check universe ownership
{
auto new_univ = csg_obj->createUniverse("new_univ");
// create cell to be auto added to root universe
std::string cname1 = "univ_cell1";
// create a universe-filled cell with name cname1, a fill of universe new_univ,
// and defined by region reg1
csg_obj->createCell(cname1, new_univ, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "univ_cell2";
csg_obj->createCell(cname2, new_univ, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a universe cell and add it to the same universe
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &add_to_univ, ®1]()
{ csg_obj->createCell("c", add_to_univ, reg1, &add_to_univ); },
"cannot be filled with the same universe to which it is being added");
}
// make lattice cells and check universe ownership
{
// create cell to be auto added to root universe
std::string cname1 = "latt_cell1";
// create a lattice-filled cell with name cname1, a fill of lattice,
// and defined by region reg1
csg_obj->createCell(cname1, lattice, reg1);
// create a cell and add to different universe, not root
std::string cname2 = "latt_cell2";
csg_obj->createCell(cname2, lattice, reg1, &add_to_univ);
// cname1 should exist in root but not the other universe
ASSERT_TRUE(root_univ.hasCell(cname1));
ASSERT_FALSE(add_to_univ.hasCell(cname1));
// cname2 should exist in add_to_univ but not root
ASSERT_TRUE(add_to_univ.hasCell(cname2));
ASSERT_FALSE(root_univ.hasCell(cname2));
}
// expected error: create a lattice cell and add it to a universe that exists in the lattice
// itself
{
Moose::UnitUtils::assertThrows(
[&csg_obj, &lattice, &lat_univ1, ®1]()
{ csg_obj->createCell("c", lattice, reg1, &lat_univ1); },
"cannot be filled with a lattice containing the same universe to which it is being added");
}
// expect error: create a cell with existing name
{
Moose::UnitUtils::assertThrows([&csg_obj, ®1]() { csg_obj->createCell("void_cell1", reg1); },
"Cell with name void_cell1 already exists");
}
}
/// tests CSG[Base/CellList]::getAllCells
TEST(CSGBaseTest, testGetAllCells)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", +s1);
csg_obj->createCell("c2", -s1);
// expect the 2 cells to be present
auto all_cells = csg_obj->getAllCells();
ASSERT_EQ(2, all_cells.size());
}
/// tests CSGBase::getCellByName / CSGCellList::getCell
TEST(CSGBaseTest, testGetCellByName)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto c1 = csg_obj->createCell("c1", +s1);
// get cell that exists
{
auto c1_get = csg_obj->getCellByName("c1");
ASSERT_EQ(c1, c1_get);
}
// try to get cell that doesn't exist in base, should raise error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getCellByName("fake_name"); },
"No cell by name fake_name exists in the geometry.");
}
}
/// tests CSG[Base/CellList]::renameCell
TEST(CSGBaseTest, testRenameCell)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// rename success
{
csg_obj->renameCell(c1, "paul");
ASSERT_EQ("paul", c1.getName());
}
// rename cell to existing name
{
// make a second cell
auto & c2 = csg_obj->createCell("c2", -s1);
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "paul"); },
"Cell with name paul already exists");
}
// rename cell that does not exist in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
// try to rename from the first base
Moose::UnitUtils::assertThrows([&csg_obj, &c2]() { csg_obj->renameCell(c2, "john"); },
"cannot be renamed to john as it does not exist");
}
}
/// tests CSGBase::updateCellRegion
TEST(CSGBaseTest, testUpdateCellRegion)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
// successfully update cell region to new region
{
csg_obj->updateCellRegion(c1, -s1);
ASSERT_EQ(-s1, c1.getRegion());
}
// try to update cell not in this base
{
// make an identical cell in a different base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c2 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &c2, &s1]() { csg_obj->updateCellRegion(c2, -s1); },
"is being updated that is different from the cell of the same "
"name in the CSGBase instance.");
}
}
/**
* Tests associated with CSGUniverseList and CSGUniverse functionality as called through CSGBase
*/
/// tests CSGBase::createUniverse
TEST(CSGBaseTest, testCreateUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
// create empty universe
{
auto & univ = csg_obj->createUniverse("thelma");
ASSERT_NO_THROW(csg_obj->getUniverseByName("thelma")); // no throw confirms existence
ASSERT_EQ(0, univ.getAllCells().size()); // confirms empty
}
// create universe from cells
{
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
// create a list of cells to be added to the universe
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
auto & univ = csg_obj->createUniverse("louise", cells);
ASSERT_NO_THROW(csg_obj->getUniverseByName("louise")); // no throw confirms existence
ASSERT_EQ(2, univ.getAllCells().size()); // confirms has cells
}
// create universe for name that already exists
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->createUniverse("louise"); },
"Universe with name louise already exists in geometry.");
}
}
/// tests CSG[Base/UniverseList]::renameUniverse and CSGBase::renameRootUniverse
TEST(CSGBaseTest, renameUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & root = csg_obj->getRootUniverse();
std::string new_name_1 = "simon";
std::string new_name_2 = "alvin";
std::string new_name_3 = "theo";
// rename root through root-specific function
{
csg_obj->renameRootUniverse(new_name_1);
ASSERT_EQ(new_name_1, root.getName());
}
// rename root by passing to method explicitly
{
csg_obj->renameUniverse(root, new_name_2);
ASSERT_EQ(new_name_2, root.getName());
}
// rename a different universe to name that already exists, should raise error
{
auto & univ = csg_obj->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_2]()
{ csg_obj->renameUniverse(univ, new_name_2); },
"Universe with name " + new_name_2 + " already exists");
}
// rename a universe that doesn't exist in the current base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj2->createUniverse("new_univ");
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &new_name_3]()
{ csg_obj->renameUniverse(univ, new_name_3); },
"cannot be renamed to " + new_name_3 + " as it does not exist");
}
}
/// tests CSGBase::addCell[s]ToUniverse
TEST(CSGBaseTest, testAddCellToUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
auto & univ = csg_obj->createUniverse("univ");
// add a list of cells to an existing universe
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2};
csg_obj->addCellsToUniverse(univ, cells);
ASSERT_EQ(2, univ.getAllCells().size());
}
// add individual cell
{
csg_obj->addCellToUniverse(univ, c3);
ASSERT_EQ(3, univ.getAllCells().size());
}
// add cell that is not in current base but has the same name and attributes, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->addCellToUniverse(univ, c4); },
"is being added to universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// add cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->addCellToUniverse(univ_new, c1); },
"Cells are being added to a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::removeCell[s]FromUniverse
TEST(CSGBaseTest, testRemoveCellFromUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
auto & c1 = csg_obj->createCell("c1", +s1);
auto & c2 = csg_obj->createCell("c2", -s1);
auto & c3 = csg_obj->createCell("c3", -s1 | +s1);
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells = {c1, c2, c3};
auto & univ = csg_obj->createUniverse("univ", cells);
// remove inidividual cell
{
csg_obj->removeCellFromUniverse(univ, c1);
ASSERT_EQ(2, univ.getAllCells().size());
}
// remove list of cells
{
std::vector<std::reference_wrapper<const CSG::CSGCell>> cells_remove = {c2, c3};
csg_obj->removeCellsFromUniverse(univ, cells_remove);
ASSERT_EQ(0, univ.getAllCells().size());
}
// remove cell that is not in current base but has the same name and attributes, should raise
// error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf2 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s2 = csg_obj2->addSurface(std::move(surf2));
auto & c4 = csg_obj2->createCell("c1", +s2);
Moose::UnitUtils::assertThrows([&csg_obj, &univ, &c4]()
{ csg_obj->removeCellFromUniverse(univ, c4); },
"is being removed from universe univ that is different from the "
"cell of the same name in the CSGBase instance.");
}
// remove cell that is in the base a universe that is not in the base, should raise error
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ_new = csg_obj2->createUniverse("univ");
Moose::UnitUtils::assertThrows(
[&csg_obj, &univ_new, &c1]() { csg_obj->removeCellFromUniverse(univ_new, c1); },
"Cells are being removed from a universe named univ that is different "
"from the universe of the same name in the CSGBase instance.");
}
}
/// tests CSGBase::get*Universe* methods
TEST(CSGBaseTest, testGetUniverse)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("harry");
// get root
{
auto & root = csg_obj->getRootUniverse();
ASSERT_TRUE(root.isRoot());
}
// successful getUniverseByName call
{
auto & univ_get = csg_obj->getUniverseByName("harry");
ASSERT_EQ(univ, univ_get);
}
// get universe for name that does not exist, expect error
{
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->getUniverseByName("potter"); },
"No universe by name potter exists in the geometry.");
}
// getAllUniverses
{
// two universes expected: ROOT_UNIVERSE and harry
auto all_univs = csg_obj->getAllUniverses();
ASSERT_EQ(2, all_univs.size());
}
}
/**
* Tests associated with CSGLattice or CSGLatticeList functionality through CSGBase
*/
/// tests the [re]setLatticeOuter methods
TEST(CSGBaseTest, testLatticeOuter)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>("lat1", 1.0);
const auto & lat = csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
// initial outer should be VOID
{
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// update to CSG_MATERIAL type
{
csg_obj->setLatticeOuter(lat, "mat_outer");
ASSERT_TRUE(lat.getOuterType() == "CSG_MATERIAL");
ASSERT_TRUE(lat.getOuterMaterial() == "mat_outer");
}
// update to UNIVERSE type
{
auto & u_out = csg_obj->createUniverse("univ_outer"); // universe for lattice outer
csg_obj->setLatticeOuter(lat, u_out);
ASSERT_TRUE(lat.getOuterType() == "UNIVERSE");
ASSERT_TRUE(lat.getOuterUniverse() == u_out);
}
// reset back to VOID
{
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(lat.getOuterType() == "VOID");
}
// try to set outer universe that is not in this base
{
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & u_out2 = csg_obj2->createUniverse("univ_outer");
Moose::UnitUtils::assertThrows([&csg_obj, &lat, &u_out2]()
{ csg_obj->setLatticeOuter(lat, u_out2); },
"Cannot set outer universe for lattice lat1. Outer universe "
"univ_outer is not in the CSGBase instance.");
}
}
/// tests CSGBase::addLattice
TEST(CSGBaseTest, testAddLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ = csg_obj->createUniverse("uni");
auto csg_obj2 = std::make_unique<CSG::CSGBase>(); // used for error checking
auto & univ2 = csg_obj2->createUniverse("uni"); // universe of same name from different base
{
// create a lattice as a unique pointer and manually add it to the CSGBase
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat =
std::make_unique<CSGCartesianLattice>("custom_lat", 1.0, univs);
// add to CSGBase
const auto & lat_ref = csg_obj->addLattice(std::move(custom_lat));
// check that it exists in the base now
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(1, all_lats.size());
ASSERT_EQ(lat_ref, all_lats[0]);
}
{
// create a custom lattice containing a universe that was not in this base (raise error)
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs2 = {{univ2}};
std::unique_ptr<CSGCartesianLattice> custom_lat2 =
std::make_unique<CSGCartesianLattice>("custom_lat2", 1.0, univs2);
// try to add to first CSGBase - raises error because universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat2]()
{ csg_obj->addLattice(std::move(custom_lat2)); },
"Cannot add lattice custom_lat2 of type "
"CSG::CSGCartesianLattice. Universe uni is not in the CSGBase "
"instance.");
}
{
// create a custom lattice with a universe outer that is not a part of this base
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ}};
std::unique_ptr<CSGCartesianLattice> custom_lat3 =
std::make_unique<CSGCartesianLattice>("custom_lat3", 1.0, univs);
// set outer universe to one from different base
custom_lat3->updateOuter(univ2);
// try to add to first CSGBase - raises error because outer universe is not in this base
Moose::UnitUtils::assertThrows([&csg_obj, &custom_lat3]()
{ csg_obj->addLattice(std::move(custom_lat3)); },
"Cannot add lattice custom_lat3 of type "
"CSG::CSGCartesianLattice. Outer universe uni is not in the "
"CSGBase instance.");
}
}
/// tests the CSGBase::setUniverseAtLatticeIndex method
TEST(CSGBaseTest, testSetUniverseAtLatticeIndex)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("spidey");
auto & univ2 = csg_obj->createUniverse("spin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("spiderverse", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid add new univ
csg_obj->setUniverseAtLatticeIndex(lat, univ2, std::make_pair<int, int>(1, 0));
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to add a universe that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("spidey");
Moose::UnitUtils::assertThrows(
[&csg_obj, &lat, &univ3]()
{ csg_obj->setUniverseAtLatticeIndex(lat, univ3, std::make_pair<int, int>(1, 0)); },
"Cannot add universe spidey to lattice spiderverse. Universe is not in the CSGBase "
"instance.");
}
}
/// tests the CSGBase::setLatticeUniverses method
TEST(CSGBaseTest, testSetLatticeUniverses)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("batman");
auto & univ2 = csg_obj->createUniverse("robin");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ1}, {univ1}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("batverse", 1.0, univs);
const auto & cartlat = csg_obj->addLattice(std::move(lat_ptr));
{
// test valid set universes - overwrite old universes
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ2},
{univ2}};
csg_obj->setLatticeUniverses(cartlat, new_univs);
auto all_univs = cartlat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ2);
ASSERT_EQ(all_univs[1][0].get(), univ2);
}
{
// try to set universes with one that is not from this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
auto & univ3 = csg_obj2->createUniverse("batman");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ3},
{univ2}};
Moose::UnitUtils::assertThrows(
[&csg_obj, &cartlat, &new_univs]() { csg_obj->setLatticeUniverses(cartlat, new_univs); },
"Cannot set universes for lattice batverse. Universe batman is not in the CSGBase "
"instance.");
}
{
// initialize a lattice without universes and then add universes with setLatticeUniverses
std::unique_ptr<CSGCartesianLattice> new_lat_ptr =
std::make_unique<CSGCartesianLattice>("new_lattice", 1.0);
const auto & lat = csg_obj->addLattice(std::move(new_lat_ptr));
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> new_univs = {{univ1},
{univ1}};
csg_obj->setLatticeUniverses(lat, new_univs);
auto all_univs = lat.getUniverses();
ASSERT_EQ(all_univs[0][0].get(), univ1);
ASSERT_EQ(all_univs[1][0].get(), univ1);
}
}
/// tests CSGBase::renameLattice
TEST(CSGBaseTest, testRenameLattice)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("original_name", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// successful rename
csg_obj->renameLattice(lat, "new_name");
ASSERT_EQ("new_name", lat.getName());
}
{
// try to rename to existing name
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
Moose::UnitUtils::assertThrows([&csg_obj, &lat2]()
{ csg_obj->renameLattice(lat2, "new_name"); },
"Lattice with name new_name already exists in geometry.");
}
{
// try to rename lattice that does not exist in this base
auto csg_obj2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr3 =
std::make_unique<CSGCartesianLattice>("another_lattice", 1.0);
const auto & lat3 = csg_obj2->addLattice(std::move(lat_ptr3));
Moose::UnitUtils::assertThrows([&csg_obj, &lat3]()
{ csg_obj->renameLattice(lat3, "some_name"); },
"another_lattice cannot be renamed to some_name as it does not "
"exist in this CSGBase instance.");
}
}
/// tests CSGBase::getLatticeByName and CSGBase::getAllLattices
TEST(CSGBaseTest, testGetLatticeMethods)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lattice1", 1.0);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
{
// get lattice by name successfully
const auto & lat_get = csg_obj->getLatticeByName<CSGCartesianLattice>("lattice1");
ASSERT_EQ(lat, lat_get);
ASSERT_EQ(typeid(lat_get), typeid(CSGCartesianLattice));
}
{
// get lattice by name without specifying type, assumes default CSGLattice
const auto & lat_get = csg_obj->getLatticeByName("lattice1");
ASSERT_EQ(lat, lat_get);
static_assert(std::is_same<decltype(lat_get), const CSGLattice &>::value);
}
{
// try to get lattice by name that does not exist
Moose::UnitUtils::assertThrows([&csg_obj]()
{ csg_obj->getLatticeByName<CSGCartesianLattice>("fake_name"); },
"No lattice by name fake_name exists in the geometry.");
}
{
// try to get lattice by name with wrong type
Moose::UnitUtils::assertThrows(
[&csg_obj]() { csg_obj->getLatticeByName<CSGHexagonalLattice>("lattice1"); },
"Cannot get lattice lattice1. Lattice is not of specified type CSG::CSGHexagonalLattice");
}
{
// get all lattices
std::unique_ptr<CSGCartesianLattice> lat_ptr2 =
std::make_unique<CSGCartesianLattice>("lattice2", 1.0);
const auto & lat2 = csg_obj->addLattice(std::move(lat_ptr2));
auto all_lats = csg_obj->getAllLattices();
ASSERT_EQ(2, all_lats.size());
ASSERT_TRUE(((all_lats[0].get() == lat) && (all_lats[1].get() == lat2)) ||
((all_lats[0].get() == lat2) && (all_lats[1].get() == lat)));
}
}
/**
* CSGBase::joinOtherBase methods
*/
/// test CSGBase::joinOtherBase no passed name
TEST(CSGBaseTest, joinOtherBaseJoinRoot)
{
// Case 1: Create two CSGBase objects to join together into a single root
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: two universes will remain
// base1 ROOT_UNIVERSE will gain all cells from base2 ROOT_UNIVERSE
// base2 ROOT_UNIVERSE will not exist as a separate universe
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
base1->joinOtherBase(std::move(base2));
// expect 3 universes: root, extra, lattice universe
// 3 cells: 2 owned by root, 1 owned by extra
ASSERT_EQ(3, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
ASSERT_EQ(2, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
ASSERT_TRUE(root.hasCell(c2.getName()));
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase one passed name
TEST(CSGBaseTest, joinOtherBaseOneNewRoot)
{
// Case 2: Create two CSGBase objects to join together but keep incoming root separate
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 4 universes will remain
// base1 ROOT_UNIVERSE and univ_in_lat will remain untouched
// all cells from ROOT_UNIVERSE in base2 create new universe called "new_univ"
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_root_name = "new_univ";
base1->joinOtherBase(std::move(base2), new_root_name);
// expect 4 universes: root, extra, new, and lat
// 3 cells: 1 owned by root, 1 owned by new, 1 owned by extra
ASSERT_EQ(4, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have c1 from original root
ASSERT_EQ(1, root.getAllCells().size());
ASSERT_TRUE(root.hasCell(c1.getName()));
// new_univ should have c2 from root of base 2
auto new_univ = base1->getUniverseByName(new_root_name);
ASSERT_EQ(1, new_univ.getAllCells().size());
ASSERT_TRUE(new_univ.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_EQ(1, new_extra.getAllCells().size());
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::joinOtherBase two passed names
TEST(CSGBaseTest, joinOtherBaseTwoNewRoot)
{
// Case 3: Create two CSGBase objects to join together with each root becoming a new universe
// CSGBase 1: only one cell containing a lattice of one universe, which lives in the ROOT_UNIVERSE
std::unique_ptr<CSGBase> base1 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr1 = std::make_unique<CSG::CSGSphere>("s1", 1.0);
const auto & surf1 = base1->addSurface(std::move(surf_ptr1));
// create a lattice of one universe
auto & univ_in_lat = base1->createUniverse("univ_in_lat");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ_in_lat}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = base1->addLattice(std::move(lat_ptr));
// create cell containing lattice
auto & c1 = base1->createCell("c1", lat, +surf1);
// CSGBase 2: two total unverses (ROOT_UNIVERSE and extra_univ) with a cell in each
std::unique_ptr<CSGBase> base2 = std::make_unique<CSG::CSGBase>();
std::unique_ptr<CSG::CSGSphere> surf_ptr2 = std::make_unique<CSG::CSGSphere>("s2", 1.0);
const auto & surf2 = base2->addSurface(std::move(surf_ptr2));
auto & c2 = base2->createCell("c2", +surf2);
auto & extra_univ = base2->createUniverse("extra_univ");
auto & c3 = base2->createCell("c3", -surf2, &extra_univ);
// Joining: 5 universes will remain
// all cells from base1 ROOT_UNIVERSE will be moved to a new universe called "new_univ1"
// all cells from base2 ROOT_UNIVERSE will be moved to a new universe called "new_univ2"
// base1 ROOT_UNIVERSE will be empty
// the "extra_univ" from base2 and "univ_in_lat" from base1 will remain separate universes
std::string new_name1 = "new_univ1";
std::string new_name2 = "new_univ2";
base1->joinOtherBase(std::move(base2), new_name1, new_name2);
// expect 5 universes: root, extra, lat, new1 and new2
// 3 cells: 0 owned by root, 1 owned by new1, 1 owned by new2, 1 owned by extra
ASSERT_EQ(5, base1->getAllUniverses().size());
auto & root = base1->getRootUniverse();
ASSERT_EQ(3, base1->getAllCells().size());
// root should have 0 cells since all were moved
ASSERT_EQ(0, root.getAllCells().size());
// new_univ1 should have c1 from original root of base 1
auto new_univ1 = base1->getUniverseByName(new_name1);
ASSERT_TRUE(new_univ1.hasCell(c1.getName()));
// new_univ2 should have c2 from original root of base 2
auto new_univ2 = base1->getUniverseByName(new_name2);
ASSERT_TRUE(new_univ2.hasCell(c2.getName()));
// original existing extra universe should still only have c3
auto & new_extra = base1->getUniverseByName("extra_univ");
ASSERT_TRUE(new_extra.hasCell(c3.getName()));
ASSERT_EQ(1, new_extra.getAllCells().size());
// expect 2 surfaces
ASSERT_EQ(2, base1->getAllSurfaces().size());
// expect 1 lattice
ASSERT_EQ(1, base1->getAllLattices().size());
}
/// test CSGBase::checkUniverseLinking / getLinkedUniverses
TEST(CSGBaseTest, testUniverseLinking)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & univ1 = csg_obj->createUniverse("univ1");
// new universe is not inherently linked to ROOT_UNIVERSE, should raise warning when checked
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ1 is not linked to root universe.");
// link the universe by adding it to a cell that is created in root
std::unique_ptr<CSG::CSGSphere> surf1 = std::make_unique<CSG::CSGSphere>("surf1", 1.0);
const auto & s1 = csg_obj->addSurface(std::move(surf1));
csg_obj->createCell("c1", univ1, +s1);
// no warning should be raised because it is a part of c1, which is a part of root
// linking tree: ROOT_UNIVERSE -> c1 -> univ1
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
// create a lattice of universes that is not linked to root, should raise warning when checked
auto & univ2 = csg_obj->createUniverse("univ2");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{univ2}};
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 1.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ2 is not linked to root universe.");
// set the outer to a universe, universe should also not be linked
auto & univ_out = csg_obj->createUniverse("univ_out");
csg_obj->setLatticeOuter(lat, univ_out);
Moose::UnitUtils::assertThrows([&csg_obj]() { csg_obj->checkUniverseLinking(); },
"Universe with name univ_out is not linked to root universe.");
// fill a new cell with the lattice, linking it to root, confirm no warning is raised when checked
// linking tree: ROOT_UNIVERSE -> c2 -> lat1 -> univ2 + univ_out
csg_obj->createCell("c2", lat, +s1);
ASSERT_NO_THROW(csg_obj->checkUniverseLinking());
}
/**
* Tests associated with CSGBase::clone
*/
/// test CSGBase::clone and equality operators for CSGBase and CSG[Surface|Cell|Universe|Lattice]List
TEST(CSGBaseTest, testCSGBaseClone)
{
auto csg_obj = std::make_unique<CSG::CSGBase>();
auto & inner_univ = csg_obj->createUniverse("univ1");
std::unique_ptr<CSG::CSGSurface> sphere_ptr_inner =
std::make_unique<CSG::CSGSphere>("inner_surf", 3.0);
auto & csg_sphere_inner = csg_obj->addSurface(std::move(sphere_ptr_inner));
csg_obj->createCell("cell_inner", "mat1", -csg_sphere_inner, &inner_univ);
// create cell with universe fill
std::unique_ptr<CSG::CSGSurface> sphere_ptr_outer =
std::make_unique<CSG::CSGSphere>("outer_surf", 5.0);
auto & csg_sphere_outer = csg_obj->addSurface(std::move(sphere_ptr_outer));
csg_obj->createCell("cell_univ_fill", inner_univ, -csg_sphere_outer);
csg_obj->createCell("cell_void", +csg_sphere_outer);
// create lattice and cell with lattice fill
auto & lat_univ = csg_obj->createUniverse("lat_univ");
std::vector<std::vector<std::reference_wrapper<const CSGUniverse>>> univs = {{lat_univ}};
auto & outer_univ = csg_obj->createUniverse("outer_univ");
std::unique_ptr<CSGCartesianLattice> lat_ptr =
std::make_unique<CSGCartesianLattice>("lat1", 2.0, univs);
const auto & lat = csg_obj->addLattice(std::move(lat_ptr));
csg_obj->setLatticeOuter(lat, outer_univ);
csg_obj->createCell("cell_lat_fill", lat, -csg_sphere_outer);
auto csg_obj_clone = csg_obj->clone();
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Add new surface to csg_obj, csg_obj and csg_obj_clone should no longer be equal
std::unique_ptr<CSG::CSGSurface> sphere_ptr_new =
std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
// Add same surface to cloned csg_obj, so that csg_obj and csg_obj_clone are equal again
sphere_ptr_new = std::make_unique<CSG::CSGSphere>("new_surf", 6.0);
csg_obj_clone->addSurface(std::move(sphere_ptr_new));
ASSERT_TRUE(*csg_obj == *csg_obj_clone);
// Reset outer universe in csg_obj and test equality of csg_obj and csg_obj_clone
csg_obj->resetLatticeOuter(lat);
ASSERT_TRUE(*csg_obj != *csg_obj_clone);
}
}
(moose/test/src/csg/ExampleCSGInfiniteSquareMeshGenerator.C)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "ExampleCSGInfiniteSquareMeshGenerator.h"
#include "CSGBase.h"
#include "CSGPlane.h"
registerMooseObject("MooseTestApp", ExampleCSGInfiniteSquareMeshGenerator);
InputParameters
ExampleCSGInfiniteSquareMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
params.addRequiredParam<Real>("side_length", "Side length of infinite square.");
params.addParam<MeshGeneratorName>(
"fill", "optional input lattice mesh generator to fill generated cell with.");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
ExampleCSGInfiniteSquareMeshGenerator::ExampleCSGInfiniteSquareMeshGenerator(
const InputParameters & params)
: MeshGenerator(params),
_side_length(getParam<Real>("side_length")),
_input_fill_name(isParamValid("fill") ? getParam<MeshGeneratorName>("fill") : ""),
_has_fill(isParamValid("fill"))
{
if (_has_fill)
{
_input_fill_mg_ptr = &getMesh("fill");
_input_fill_csg = &getCSGBase("fill");
}
}
std::unique_ptr<MeshBase>
ExampleCSGInfiniteSquareMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
ExampleCSGInfiniteSquareMeshGenerator::generateCSG()
{
// name of the current mesh generator to use for naming generated objects
auto mg_name = this->name();
// initialize a CSGBase object
auto csg_obj = std::make_unique<CSG::CSGBase>();
// Add surfaces and halfspaces corresponding to 4 planes of infinite square
std::vector<std::vector<Point>> points_on_planes{{Point(1. * _side_length / 2., 0., 0.),
Point(1. * _side_length / 2., 1., 0.),
Point(1. * _side_length / 2., 0., 1.)},
{Point(-1. * _side_length / 2., 0., 0.),
Point(-1. * _side_length / 2., 1., 0.),
Point(-1. * _side_length / 2., 0., 1.)},
{Point(0., 1. * _side_length / 2., 0.),
Point(1., 1. * _side_length / 2., 0.),
Point(0., 1. * _side_length / 2., 1.)},
{Point(0., -1. * _side_length / 2., 0.),
Point(1., -1. * _side_length / 2., 0.),
Point(0., -1. * _side_length / 2., 1.)}};
std::vector<std::string> surf_names{"plus_x", "minus_x", "plus_y", "minus_y"};
// initialize cell region to be updated
CSG::CSGRegion region;
// set the center of the prism to be used for determining half-spaces
const auto centroid = Point(0, 0, 0);
for (unsigned int i = 0; i < points_on_planes.size(); ++i)
{
// object name includes the mesh generator name for uniqueness
const auto surf_name = mg_name + "_surf_" + surf_names[i];
// create the plane for one face of the prism
std::unique_ptr<CSG::CSGSurface> plane_ptr = std::make_unique<CSG::CSGPlane>(
surf_name, points_on_planes[i][0], points_on_planes[i][1], points_on_planes[i][2]);
auto & csg_plane = csg_obj->addSurface(std::move(plane_ptr));
// determine where the plane is in relation to the centroid to be able to set the half-space
const auto region_direction = csg_plane.getHalfspaceFromPoint(centroid);
// half-space is either positive (+plane_ptr) or negative (-plane_ptr)
// depending on the direction to the centroid
auto halfspace =
((region_direction == CSG::CSGSurface::Halfspace::POSITIVE) ? +csg_plane : -csg_plane);
// check if this is the first half-space to be added to the region,
// if not, update the existing region with the intersection of the regions (&=)
if (region.getRegionType() == CSG::CSGRegion::RegionType::EMPTY)
region = halfspace;
else
region &= halfspace;
}
// create the cell defined by the surfaces and region just created
const auto cell_name = mg_name + "_square_cell";
// determine fill: either from input fill mesh generator or default material
if (_has_fill)
{
// join the fill CSGBase into the current CSGBase & use the lattice as the fill
csg_obj->joinOtherBase(std::move(*_input_fill_csg));
// assume input MG is a lattice type for sake of this example/test
const CSG::CSGLattice & lattice = csg_obj->getLatticeByName(_input_fill_name + "_lattice");
csg_obj->createCell(cell_name, lattice, region);
}
else // default material fill
{
const auto material_name = "square_material";
csg_obj->createCell(cell_name, material_name, region);
}
return csg_obj;
}
(moose/test/src/csg/TestCSGAxialSurfaceMeshGenerator.C)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "TestCSGAxialSurfaceMeshGenerator.h"
#include "MeshGenerator.h"
#include "CSGPlane.h"
registerMooseObject("MooseTestApp", TestCSGAxialSurfaceMeshGenerator);
InputParameters
TestCSGAxialSurfaceMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
// input parameter that is an existing mesh generator
params.addRequiredParam<MeshGeneratorName>("input", "The input MeshGenerator.");
// additional params for this specific mesh generator
params.addRequiredParam<Real>("axial_height", "Axial height of the model.");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
TestCSGAxialSurfaceMeshGenerator::TestCSGAxialSurfaceMeshGenerator(const InputParameters & params)
: MeshGenerator(params),
_mesh_ptr(getMesh("input")),
_axial_height(getParam<Real>("axial_height"))
{
_build_csg = &getCSGBase("input");
}
std::unique_ptr<MeshBase>
TestCSGAxialSurfaceMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
TestCSGAxialSurfaceMeshGenerator::generateCSG()
{
// get the existing CSGBase associated with the input mesh generator
// this is the CSGBase object that will be updated
std::unique_ptr<CSG::CSGBase> csg_obj = std::move(*_build_csg);
// get the names of the current mesh generator and the input mesh generator
// so that unique object naming can be enforced
auto mg_name = this->name();
auto inp_name = getParam<MeshGeneratorName>("input");
// get the expected existing cell
const auto cell_name = inp_name + "_square_cell";
const auto & csg_cell = csg_obj->getCellByName(cell_name);
// get the existing cell region to update
auto cell_region = csg_cell.getRegion();
// centroid used to determine direction for half-space
const auto centroid = Point(0, 0, 0);
// setting a default surface name purely for testing purposes
const auto default_surf_name = "default_surf";
// Add surfaces and halfspaces corresponding to top and bottom axial planes
std::vector<std::string> surf_names{"plus_z", "minus_z"};
std::vector<Real> coeffs{0.5 * _axial_height, -0.5 * _axial_height};
for (unsigned int i = 0; i < coeffs.size(); ++i)
{
// create a plane using the coefficients for the equation of a plane
// z plane equation: 0.0*x + 0.0*y + 1.0*z = (+/-)0.5 * axial_height
std::unique_ptr<CSG::CSGSurface> surface_ptr =
std::make_unique<CSG::CSGPlane>(default_surf_name, 0.0, 0.0, 1.0, coeffs[i]);
auto & csg_plane = csg_obj->addSurface(std::move(surface_ptr));
// Rename surface so that it has a unique surface name based on the mesh generator
const auto surf_name = mg_name + "_surf_" + surf_names[i];
csg_obj->renameSurface(csg_plane, surf_name);
// determine the half-space to add as an updated intersection
const auto region_direction = csg_plane.getHalfspaceFromPoint(centroid);
auto halfspace =
((region_direction == CSG::CSGSurface::Halfspace::POSITIVE) ? +csg_plane : -csg_plane);
// update the existing region with a half-space
cell_region &= halfspace;
}
// set the new region for the existing cell
csg_obj->updateCellRegion(csg_cell, cell_region);
// Rename cell as it now defines a box region instead of an infinite square region
csg_obj->renameCell(csg_cell, mg_name + "_box_cell");
return csg_obj;
}
(moose/test/tests/csg/csg_only_chained.i)
[Mesh]
[inf_square]
type = ExampleCSGInfiniteSquareMeshGenerator
side_length = 4
[]
[cube]
type = TestCSGAxialSurfaceMeshGenerator
input = inf_square
axial_height = 5
[]
[]
(moose/test/tests/csg/gold/csg_only_chained_out_csg.json)
{
"cells": {
"cube_box_cell": {
"fill": "square_material",
"filltype": "CSG_MATERIAL",
"region":
"(+inf_square_surf_plus_x & -inf_square_surf_minus_x & -inf_square_surf_plus_y & +inf_square_surf_minus_y & -cube_surf_plus_z & +cube_surf_minus_z)"
}
},
"surfaces": {
"inf_square_surf_minus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": 2.0
},
"type": "CSG::CSGPlane"
},
"inf_square_surf_minus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": -2.0
},
"type": "CSG::CSGPlane"
},
"cube_surf_minus_z": {
"coefficients": {
"a": 0.0,
"b": 0.0,
"c": 1.0,
"d": -2.5
},
"type": "CSG::CSGPlane"
},
"inf_square_surf_plus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": -2.0
},
"type": "CSG::CSGPlane"
},
"inf_square_surf_plus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": 2.0
},
"type": "CSG::CSGPlane"
},
"cube_surf_plus_z": {
"coefficients": {
"a": 0.0,
"b": 0.0,
"c": 1.0,
"d": 2.5
},
"type": "CSG::CSGPlane"
}
},
"universes": {
"ROOT_UNIVERSE": {
"cells": [
"cube_box_cell"
],
"root": true
}
}
}
(moose/test/src/csg/TestCSGLatticeMeshGenerator.C)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#include "TestCSGLatticeMeshGenerator.h"
#include "MeshGenerator.h"
#include "CSGPlane.h"
#include "CSGCartesianLattice.h"
#include "CSGHexagonalLattice.h"
registerMooseObject("MooseTestApp", TestCSGLatticeMeshGenerator);
InputParameters
TestCSGLatticeMeshGenerator::validParams()
{
InputParameters params = MeshGenerator::validParams();
// input parameter that is an existing mesh generator
params.addRequiredParam<std::vector<MeshGeneratorName>>(
"inputs",
"The MeshGenerators that form the components of the lattice. Order of inputs corresponds to "
"the associated integer ID for the pattern (i.e., 0 for first input, 1 for second input, "
"etc.)");
params.addRequiredParam<std::string>(
"lattice_type", "The type of lattice to create. Options are 'cartesian' and 'hexagonal'.");
params.addRequiredParam<Real>("pitch",
"The pitch (flat-to-flat distance) of each lattice element.");
params.addRequiredParam<std::vector<std::vector<unsigned int>>>(
"pattern",
"A double-indexed array starting with the upper-left corner where the index"
"represents the index of the mesh/CSG generator in the 'inputs' vector");
// Declare that this generator has a generateCSG method
MeshGenerator::setHasGenerateCSG(params);
return params;
}
TestCSGLatticeMeshGenerator::TestCSGLatticeMeshGenerator(const InputParameters & params)
: MeshGenerator(params),
_lattice_type(getParam<std::string>("lattice_type")),
_pitch(getParam<Real>("pitch")),
_input_names(getParam<std::vector<MeshGeneratorName>>("inputs")),
_mesh_ptrs(getMeshes("inputs")),
_pattern(getParam<std::vector<std::vector<unsigned int>>>("pattern"))
{
for (auto inp : _input_names)
_input_csgs.push_back(&getCSGBaseByName(inp));
}
std::unique_ptr<MeshBase>
TestCSGLatticeMeshGenerator::generate()
{
auto null_mesh = nullptr;
return null_mesh;
}
std::unique_ptr<CSG::CSGBase>
TestCSGLatticeMeshGenerator::generateCSG()
{
// create a new CSGBase object to build the lattice in
auto csg_obj = std::make_unique<CSG::CSGBase>();
// get the name of the current mesh generator
auto mg_name = this->name();
// join each input CSGBase into the new CSGBase as a unique universe
std::unordered_map<unsigned int, std::string> univ_id_names;
for (const auto i : index_range(_input_names))
{
std::string join_name = _input_names[i] + "_univ";
csg_obj->joinOtherBase(std::move(*_input_csgs[i]), join_name);
univ_id_names[i] = join_name;
}
// build the universe pattern for the lattice using the input pattern
std::vector<std::vector<std::reference_wrapper<const CSG::CSGUniverse>>> universe_pattern;
for (const auto & row : _pattern)
{
std::vector<std::reference_wrapper<const CSG::CSGUniverse>> universe_row;
for (const auto univ_id : row)
{
const auto & univ = csg_obj->getUniverseByName(univ_id_names[univ_id]);
universe_row.push_back(univ);
}
universe_pattern.push_back(universe_row);
}
// create the lattice based on the specified type
std::string lat_name = mg_name + "_lattice";
if (_lattice_type == "cartesian")
{
std::unique_ptr<CSG::CSGCartesianLattice> lat_ptr =
std::make_unique<CSG::CSGCartesianLattice>(lat_name, _pitch, universe_pattern);
csg_obj->addLattice<CSG::CSGCartesianLattice>(std::move(lat_ptr));
}
else if (_lattice_type == "hexagonal")
{
std::unique_ptr<CSG::CSGHexagonalLattice> lat_ptr =
std::make_unique<CSG::CSGHexagonalLattice>(lat_name, _pitch, universe_pattern);
csg_obj->addLattice<CSG::CSGHexagonalLattice>(std::move(lat_ptr));
}
return csg_obj;
}
(moose/test/tests/csg/csg_lattice_cart.i)
[Mesh]
[sq1]
type = ExampleCSGInfiniteSquareMeshGenerator
side_length = 4
[]
[sq2]
type = ExampleCSGInfiniteSquareMeshGenerator
side_length = 3
[]
[cart_lat]
type = TestCSGLatticeMeshGenerator
lattice_type = 'cartesian'
inputs = 'sq1 sq2'
pattern = '0 0;
0 1'
pitch = 5
[]
[sq3]
type = ExampleCSGInfiniteSquareMeshGenerator
side_length = 15
fill = 'cart_lat'
[]
[]
(moose/test/tests/csg/gold/csg_lattice_cart_out_csg.json)
{
"cells": {
"sq1_square_cell": {
"fill": "square_material",
"filltype": "CSG_MATERIAL",
"region": "(+sq1_surf_plus_x & -sq1_surf_minus_x & -sq1_surf_plus_y & +sq1_surf_minus_y)"
},
"sq2_square_cell": {
"fill": "square_material",
"filltype": "CSG_MATERIAL",
"region": "(+sq2_surf_plus_x & -sq2_surf_minus_x & -sq2_surf_plus_y & +sq2_surf_minus_y)"
},
"sq3_square_cell": {
"fill": "cart_lat_lattice",
"filltype": "LATTICE",
"region": "(+sq3_surf_plus_x & -sq3_surf_minus_x & -sq3_surf_plus_y & +sq3_surf_minus_y)"
}
},
"lattices": {
"cart_lat_lattice": {
"attributes": {
"ncol": 2,
"nrow": 2,
"pitch": 5.0
},
"outertype": "VOID",
"type": "CSG::CSGCartesianLattice",
"universes": [
[
"sq1_univ",
"sq1_univ"
],
[
"sq1_univ",
"sq2_univ"
]
]
}
},
"surfaces": {
"sq1_surf_minus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": 2.0
},
"type": "CSG::CSGPlane"
},
"sq1_surf_minus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": -2.0
},
"type": "CSG::CSGPlane"
},
"sq1_surf_plus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": -2.0
},
"type": "CSG::CSGPlane"
},
"sq1_surf_plus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": 2.0
},
"type": "CSG::CSGPlane"
},
"sq2_surf_minus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": 1.5
},
"type": "CSG::CSGPlane"
},
"sq2_surf_minus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": -1.5
},
"type": "CSG::CSGPlane"
},
"sq2_surf_plus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": -1.5
},
"type": "CSG::CSGPlane"
},
"sq2_surf_plus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": 1.5
},
"type": "CSG::CSGPlane"
},
"sq3_surf_minus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": 7.5
},
"type": "CSG::CSGPlane"
},
"sq3_surf_minus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": -7.5
},
"type": "CSG::CSGPlane"
},
"sq3_surf_plus_x": {
"coefficients": {
"a": -1.0,
"b": 0.0,
"c": 0.0,
"d": -7.5
},
"type": "CSG::CSGPlane"
},
"sq3_surf_plus_y": {
"coefficients": {
"a": 0.0,
"b": 1.0,
"c": 0.0,
"d": 7.5
},
"type": "CSG::CSGPlane"
}
},
"universes": {
"ROOT_UNIVERSE": {
"cells": [
"sq3_square_cell"
],
"root": true
},
"sq1_univ": {
"cells": [
"sq1_square_cell"
]
},
"sq2_univ": {
"cells": [
"sq2_square_cell"
]
}
}
}